



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
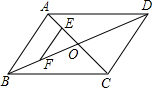 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )| A、6 | B、4 | C、3 | D、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
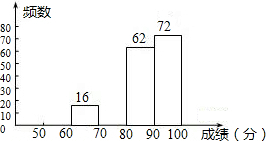 某区八年级有3000名学生参加“心理健康知识竞赛”活动.
某区八年级有3000名学生参加“心理健康知识竞赛”活动.| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | 0.2 | |
| 80≤x<90 | 62 | |
| 90≤x<100 | 72 | 0.36 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 模拟中招体育成绩(分数段)统计表 |  | ||
| 分数段 | 人数(人) | 频率 | |
| A | 60 | 0.2 | |
| B | a | 0.25 | |
| c | 90 | 0.30 | |
| D | 48 | b | |
| E | 27 | 0.09 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com