
如图,在平面直角坐标系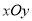 中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC. 若A点的坐标为(
中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC. 若A点的坐标为(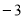 ,1),B、C两点的纵坐标均为
,1),B、C两点的纵坐标均为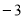 ,D、E两点在
,D、E两点在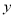 轴上.
轴上.
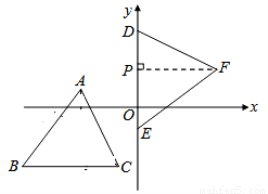
(1)、求证:等腰△BCA两腰上的高相等;
(2)、求△BCA两腰上高线的长;
(3)、求△DEF的高线FP的长.
(1)、见解析;(2)、4;(3)、4.
【解析】
试题分析:(1)、分别作高线AH、CK,判定△AKC和△CHA全等得出结论;(2)、根据点A、B、C的坐标求出AH的长度,然后结合第一题的结论求出结果;(3)、根据三角形全等的条件判定出△AKC和△DPF全等,从而得出所求的线段.
试题解析:(1)在△ABC中,分别作高线AH、CK,则∠AKC=∠CHA=90°.
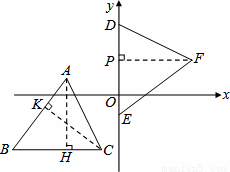
∵AB=BC,∴∠BAC=∠BCA.
在△AKC和△CHA中,∵∠AKC=∠CHA,∠BAC=∠BCA,AC=CA,
∴△AKC≌△CHA(AAS)∴CK=AH.
(2)、∵A点的坐标为(-3,1),B、C两点的纵坐标均为-3, ∴AH=4.
又∵CK=AH, ∴CK=AH =4.
(3)、∵△ABC≌△DEF,∴∠BAC=∠EDF,AC=DF.
在△AKC和△DPF中,∠AKC=∠DPF=90°,∠BAC=∠EDF,AC=DF,
∴△AKC≌△DPF(AAS). ∴PF=KC=4.
考点:三角形全等的证明与性质.


科目:初中数学 来源:2014-2015学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:解答题
已知A,B,C三点在同一条数轴上.
(1)、若点A,B表示的数分别为-4,2,且BC=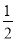 AB,则点C表示的数是 ;
AB,则点C表示的数是 ;
(2)、点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC=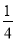 BD,求线段AD的长(用含m,n的式子表示).
BD,求线段AD的长(用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:选择题
已知关于x的方程2x+2m=5的解是x=-2,则m的值为( ).
A.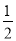 B.-
B.-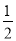 C.
C.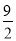 D. -
D. -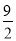
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区八年级上学期期末考试数学试卷(解析版) 题型:填空题
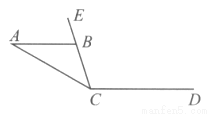
如图,AB∥CD,点E在CB的延长线上. 若∠ABE=70°,则∠ECD= 度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省诸城市九年级下学期开学检测数学试卷(解析版) 题型:解答题
(本题满分10分)某校在周二至周四的课余时间分别开设了“国学”、“拉丁舞”、“机器人”三门选修课课程.
(1)若小莹任意选修其中两门课程,求选修两门课程中含有国学的概率?
(2)若小莹和小亮各自任意选修一门课程,求两人选修同一门课程的概率?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:选择题
-只不透明的袋子中装有1个白球和2个红球,这些球除了颜色外都相同,搅匀后从中任意摸出一球,记录颜色后放回、搅匀,再从中任意摸出一球,那么,两次都摸到红球的概率为( )
A.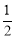 B.
B.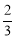 C.
C.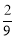 D.
D.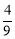
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com