
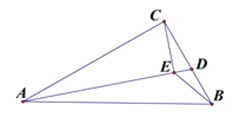
【题目】如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是( )
A.2.5B.![]()
![]() C.
C.![]() D.5
D.5
【答案】C
【解析】
由∠AEC=90°知E在以AC为直径的⊙M的![]() 上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC,根据相似三角形的性质得到MF,根据勾股定理得到AF,BF,BM,于是得到结论.
上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC,根据相似三角形的性质得到MF,根据勾股定理得到AF,BF,BM,于是得到结论.
解:如图,取AC的中点M,以AC为直径作圆M,交AB于点N,连接BM,交圆M于点E′,过M作MF⊥AB于点F,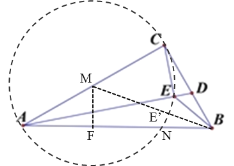
由题意知,∠AEC=90°,
∴E在以AC为直径的⊙M的![]() 上(不含点C、可含点N),
上(不含点C、可含点N),
∴BE最短时,即为连接BM与⊙M的交点(图中点E′点),
∵AB=13cm,AC=12cm,BC=5cm,
∴AC2+BC2=AB2,AM=CM=6
∴∠ACB=90°,
作MF⊥AB于F,
∴∠AFM=∠ACB=90°,∠FAM=∠CAB,
∴△AMF∽△ABC,
∴![]() ,即
,即![]() ,解得:MF=
,解得:MF=![]() ,
,
∴AF=![]() ,
,
则BF=ABAF=![]() ,
,
∴BM=![]() ,
,
∵ME=6,
∴BE长度的最小值BE′=BMME′=![]() ,
,
故答案为:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于
轴交于![]() 和
和![]() ,与
,与 ![]() 轴交于
轴交于 ![]() 点,点
点,点![]() 关于抛物线的对称轴的对称点为点
关于抛物线的对称轴的对称点为点![]() .
.
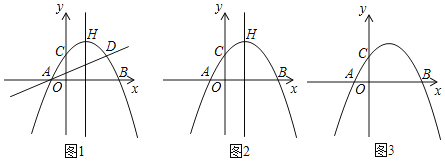
(1)求此抛物线的解析式和对称轴.
(2)如图 2,当点![]() 在抛物线的对称轴上运动时,在直线
在抛物线的对称轴上运动时,在直线![]() 上是否存在点
上是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)如图 3,当点![]() 、
、![]() 、
、![]() 三点共圆时,请求出该圆圆心的坐标.
三点共圆时,请求出该圆圆心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
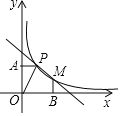
【题目】如图,已知反比例函数![]() 的图象和一次函数
的图象和一次函数![]() 的图象都过点
的图象都过点![]() ,过点P作y轴的垂线,垂足为A,O为坐标原点,
,过点P作y轴的垂线,垂足为A,O为坐标原点,![]() 的面积为1.
的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
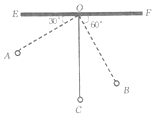
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在![]() 的位置时俯角
的位置时俯角![]() ,在
,在![]() 的位置时俯角
的位置时俯角![]() ,若
,若![]() ,点
,点![]() 比点
比点![]() 高7
高7![]() .
.
求:(1)单摆的长度;
(2)从点![]() 摆动到点
摆动到点![]() 经过的路径长.(要求:本题中的计算结果均保留整数.参考值:
经过的路径长.(要求:本题中的计算结果均保留整数.参考值:![]() ;
;![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
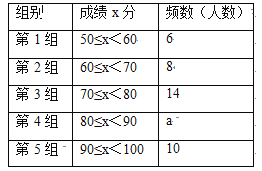
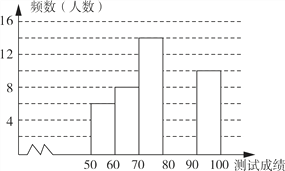
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世园会开园期间,为了满足不同人群的游览需求,组委会倾情打造了四条趣玩路线,分别是“解密世园会”、“爱我家,爱园艺”、“园艺小清新之旅”和“快速车览之旅”小明一家想通过抽签的方法选择其中的两条路线进行游玩,于是他们制作了如下四张卡片,然后从四张卡片中随机抽取其中的两张若小明最钟爱的游玩路线是“园艺小清新之旅",小明的爸爸和妈妈最钟爱的游玩路线是“解密世园会”,请用列表法或画树状图法求出:他们同时抽中“园艺小清新之旅”和“解密世园会”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
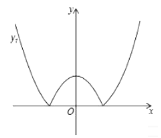
【题目】如图,将二次函数![]() (其中
(其中![]() )的图象在
)的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,形成新的图象记为
轴翻折,图象的其余部分保持不变,形成新的图象记为![]() ,另有一次函数
,另有一次函数![]() 的图象记为
的图象记为![]() ,若
,若![]() 与
与![]() 恰有两个交点时,则
恰有两个交点时,则![]() 的范围是________.
的范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
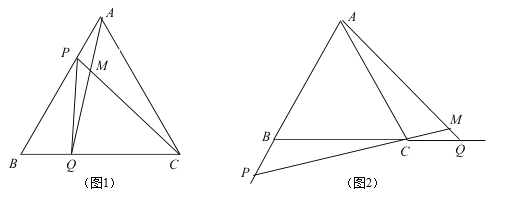
【题目】如图(1),点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是1cm/s
(1)设运动时间是t,则当t=__________s时,△PBQ是直角三角形.
(2)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)如图(2),若P,Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com