
分析 原式约分后,将已知等式变形为a2=-3a+1,代入计算即可求出值.
解答 解:∵a2+3a-1=0,即a2=-3a+1,
∴原式=$\frac{{a}^{4}}{{a}^{2}({a}^{4}-3{a}^{2}+1)}$=$\frac{{a}^{2}}{{a}^{4}-3{a}^{2}+1}$=$\frac{-3a+1}{(-3a+1)^{2}+9a-3+1}$=$\frac{-3a+1}{9{a}^{2}+3a-1}$=$\frac{-3a+1}{-27a+9+3a-1}$=$\frac{-3a+1}{-24a+8}$=$\frac{-3a+1}{8(-3a+1)}$=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
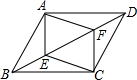 已知:如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,求证:四边形AECF是平行四边形;
已知:如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,求证:四边形AECF是平行四边形;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com