
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
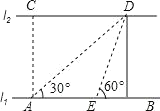
【答案】C、D两点间的距离为30m.
【解析】直接利用等腰三角形的判定与性质得出DE=AE=20,进而求出EF的长,再得出四边形ACDF为矩形,则CD=AF=AE+EF求出答案.
解:过点D作l1的垂线,垂足为F,
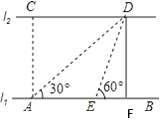
∵∠DEB=60°,∠DAB=30°,
∴∠ADE=∠DEB﹣∠DAB=30°,
∴△ADE为等腰三角形,
∴DE=AE=20,
在Rt△DEF中,EF=DEcos60°=20×![]() =10,
=10,
∵DF⊥AF,
∴∠DFB=90°,
∴AC∥DF,由已知l1∥l2,
∴CD∥AF,
∴四边形ACDF为矩形,CD=AF=AE+EF=30,
答:C、D两点间的距离为30m
“点睛”此题考查了两点之间的距离以及等腰三角形的判定与性质以及锐角三角函数关系,得出EF的长是解题关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】已知直线![]() (k>0)与双曲线
(k>0)与双曲线![]() (x>0)交于点M、N,且点N的横坐标为k. .
(x>0)交于点M、N,且点N的横坐标为k. .
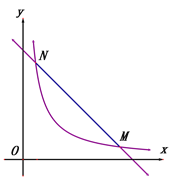
(1) 如图1,当k=1时.
①求m的值及线段MN的长;
②在y轴上是否是否存在点Q,使∠MQN=90°,若存在,请求出点Q的坐标;若不存在,请说明理由.
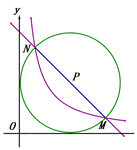
(2) 如图2,以MN为直径作⊙P,当⊙P与y轴相切时,求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 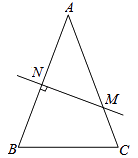
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张大伯从报社以每份0.4元的价格购进了a份报纸,以每份0.5元的价格售出了b份报纸,剩余的以每份0.2元的价格退回报社,则张大伯卖报收入元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为![]() (△ABD、△ADC的面积分别用记号
(△ABD、△ADC的面积分别用记号![]() 、
、![]() 表示).现有
表示).现有![]() ,则
,则![]() .
.
(2)如图2,△ABC中,E、F分别是BC、AC边上一点,且有![]() ,
, ![]() ,AE与BF相交于点G.现作EH∥BF交AC于点H.依次求
,AE与BF相交于点G.现作EH∥BF交AC于点H.依次求![]() 、
、![]() 、
、![]() 的值.
的值.
(3)如图3,△ABC中,点P在边AB上,点M、N在边AC上,且有![]() ,
, ![]() ,
,
BM、BN与CP分别相交于点R、Q.现已知△ABC的面积为1,求△BRQ的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值。
(1)已知x+y=15,x2+y2=113,求x2﹣xy+y2的值.
(2)先化简,再求值: ![]() ÷
÷ ![]() +1,在0,1,2,三个数中选一个合适的,代入求值.
+1,在0,1,2,三个数中选一个合适的,代入求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com