
【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON.
【答案】
(1)解:逆命题是:到角两边距离相等的点在这个角的平分线上,题设是到角两边距离相等的点,结论是该点在这个角的平分线上
(2)解:如图:
根据题意作出图形,由AB是一直线,即可求出∠AOB=180°,然后根据角平分线的性质,推出 ∠ M O C = ![]() ∠ A O C , ∠ N O C =
∠ A O C , ∠ N O C = ![]() ∠ B O C ,则 ∠ M O N = ∠ M O N + ∠ N O C =
∠ B O C ,则 ∠ M O N = ∠ M O N + ∠ N O C = ![]() ∠ A O B = 90 ° 即可.
∠ A O B = 90 ° 即可.
该命题的文字描述是:邻补角的平分线互相垂直
【解析】(1),找出原命题的题设与结论,然后将其互换便可写出原命题的逆命题;接下来根据题设和结论的定义写出逆命题的题设和结论;
(2)根据题意作出图形,利用角平分线性质得出 ∠ M O C = ![]() ∠ A O C , ∠ N O C =
∠ A O C , ∠ N O C = ![]() ∠ B O C ,再根据邻补角的知识得出 ∠ M O N = ∠ M O N + ∠ N O C =
∠ B O C ,再根据邻补角的知识得出 ∠ M O N = ∠ M O N + ∠ N O C = ![]() ∠ A O B = 90 ° ,从而得出结论。
∠ A O B = 90 ° ,从而得出结论。


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.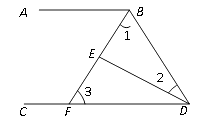
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( ) 
A.3 cm
B.4 cm
C.5 cm
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古城黄州以其名胜古迹吸引了不少游客.从地图上看,较有名的六外景点在黄州城内的分布是∶东坡赤壁在市政府以西2km再往南3km处,黄冈中学在市政府以东1 km处,宝塔公园在市政府以东3km处,鄂黄长江桥在市政府以东7 km再往北8 km处,遗爱湖在市政府以东4km再往北4km处,博物馆在市政府以北2 km再往西1 km处。请画图表示出这六个景点的位置,并用坐标表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
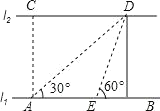
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?代数式:(m+n)2 , (m﹣n)2 , mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,C,对称轴是x=﹣3,请解答下列问题:
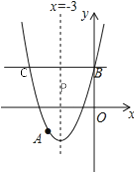
(1)求抛物线的解析式.
(2)求点B的坐标;
(3)过点B作与x轴平行的直线交抛物线交点C,在抛物线的对称轴上的确存在一点P,使PA+PC的值最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B.C.D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.
①△BCE≌△ACD;
②CF=CH;
③△CFH为等边三角形;
④FH∥BD;
⑤AD与BE的夹角为60°,
以上结论正确的是 . 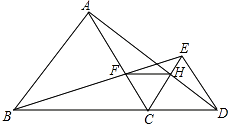
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com