Question

【题目】如图，抛物线y=x2+bx+c过点A（﹣4，﹣3），与y轴交于点B，C，对称轴是x=﹣3，请解答下列问题：

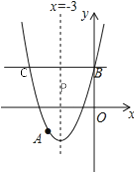
（1）求抛物线的解析式．

（2）求点B的坐标；

（3）过点B作与x轴平行的直线交抛物线交点C，在抛物线的对称轴上的确存在一点P，使PA+PC的值最小，求点P的坐标．

Answer 1

【答案】（1）；（2）B点坐标为（0,5）；（3）P（-3，-1）

【解析】（1）根据对称轴是x=﹣3，求出b=6，把点A（﹣4，﹣3）代入y=x2+bx+c得16﹣4b+c=﹣3，即可得出答案；（2）利用待定系数法求出一次函数关系式即可求出点P的坐标．

解：（1）把点A（-4，-3）代入y=x+bx+c得16-4b+c=-3，即c-4b=-19，

∵对称轴为直线x=-3，

∴，解得b=6，

∴c=-19+4b=5，

∴抛物线的解析式是

令x=0,则y=5 ∴B点坐标为（0,5）.

（2）如图所示，

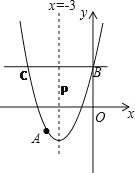
∵BC∥x轴，

∴点C与点B关于直线x=-3对称，即直线x=-3是线段BC的垂直平分线.

连接AB交抛物线对称轴于点P,连接CP，这时PC=PB，PA+PC=PA+PB=AB

∴点P为题意的点.

设AB的表达式为，把A（-4，-3）、B（0，5）代入得：

，解得∴

在中，令x=-3得y=-1，∴P（-3，-1）