
分析 首先通分,然后根据同分母分式加减法法则,求出算式$\frac{2x}{{x}^{2}-3x}$+$\frac{1}{{x}^{2}-9}$的值是多少即可.
解答 解:$\frac{2x}{{x}^{2}-3x}$+$\frac{1}{{x}^{2}-9}$
=$\frac{2}{x-3}$+$\frac{1}{{x}^{2}-9}$
=$\frac{2(x+3)}{{x}^{2}-9}$+$\frac{1}{{x}^{2}-9}$
=$\frac{2x+7}{{x}^{2}-9}$.
点评 此题主要考查了分式的加减法,要熟练掌握,解答此题的关键是要明确:(1)同分母分式加减法法则:同分母的分式相加减,分母不变,把分子相加减.(2)异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 第三、四象限 | B. | 第一、二象限 | C. | 第二、三象限 | D. | 第一、二、三象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.14×108 | B. | 1.4×107 | C. | 1.4×108 | D. | 14×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
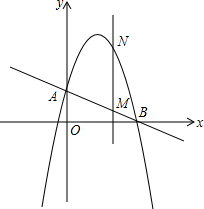 如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO=$\frac{1}{2}$,抛物线y=-x2+bx+c过A、B两点.
如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO=$\frac{1}{2}$,抛物线y=-x2+bx+c过A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
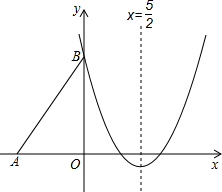 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
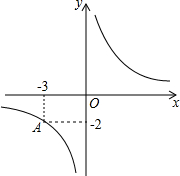 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-2)(a-8) | B. | (a+2)(a-8) | C. | (a-2)(a+8) | D. | (a+2)(a+8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com