
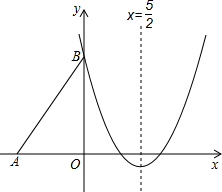
 ��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=$\frac{2}{3}$x2+bx+c������B���Ҷ�����ֱ��x=$\frac{5}{2}$�ϣ�
��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=$\frac{2}{3}$x2+bx+c������B���Ҷ�����ֱ��x=$\frac{5}{2}$�ϣ����� ��1�����öԳ��ṫʽ���b��ֵ��������B������ó�c���ɣ�
��2���������ε����ʵó�C��D�����꣬������ͼ���ϵ���������ʵó��𰸣�
��3���������CD����ֱ�߽���ʽ��������ԳƵó�P��λ�ã������ó�P�����꣮
��� �⣺��1����������y=$\frac{2}{3}$x2+bx+c����B��0��4����
��c=4��
�߶�����ֱ��x=$\frac{5}{2}$�ϣ���-$\frac{b}{2a}$=$\frac{5}{2}$����-$\frac{b}{2��\frac{2}{3}}$=$\frac{5}{2}$��
��ã�b=-$\frac{10}{3}$��
������ĺ�����ϵʽΪ��y=$\frac{2}{3}$x2-$\frac{10}{3}$x+4��
��2����ͼ��ʾ����Rt��ABO�У�OA=3��OB=4����AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5��
���ı���ABCD�����Σ���BC=CD=DA=AB=5��
��C��D���������ֱ��ǣ�5��4������2��0����
��x=5ʱ��y=$\frac{2}{3}$��52-$\frac{10}{3}$��5+4=4��
��x=2ʱ��y=$\frac{2}{3}$��22-$\frac{10}{3}$��2+4=0��
���C�͵�D���������������ϣ�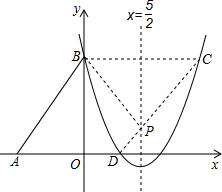
��3���ɣ�2����֪����B���C���ڶԳ���Գƣ�
��CD��Գ��ύ�ڵ�P����PΪ����ĵ㣬
��ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b��
��$\left\{\begin{array}{l}{5k+b=4}\\{2k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{8}{3}}\end{array}\right.$��
��ֱ��CD��Ӧ�ĺ�����ϵʽΪ��y=$\frac{4}{3}$x-$\frac{8}{3}$��
��x=$\frac{5}{2}$ʱ��y=$\frac{4}{3}$��$\frac{5}{2}$-$\frac{8}{3}$=$\frac{2}{3}$��
��P��$\frac{5}{2}$��$\frac{2}{3}$����
���� ������Ҫ�����˶��κ����ۺ��Լ����ɶ��������ε����ʵ�֪ʶ��������Գ����P��λ���ǽ���ؼ���


 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
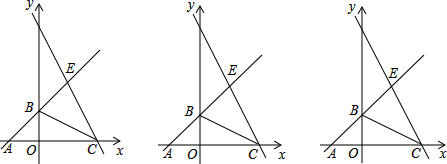
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.18��109Ԫ | B�� | 21.8��108Ԫ | C�� | 2.176��109Ԫ | D�� | 21.76��108Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
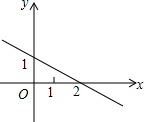 ������y=kx+b��k��bΪ��������ͼ����ͼ��ʾ����ô��y��0ʱ��x��ȡֵ��Χ�ǣ�������
������y=kx+b��k��bΪ��������ͼ����ͼ��ʾ����ô��y��0ʱ��x��ȡֵ��Χ�ǣ�������| A�� | x��2 | B�� | x��2 | C�� | x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com