

���� ��1�����ݵ���ֱ�������ε����ʼ��ɵõ����ۣ�
��2���ɵ��������ε����ʺ�ֱ�������ε����ʼ��ɵõ����ۣ�
��3�����������PB=DQ=t��CP=CQ=3-t��Ȼ����ݵ��������ε����ʺ��ɶ������ɽ�������
���������BP=DQ=tcm�����ı���ABCD�������Σ��õ�AB=AD����ABP=��ADQ���Ƴ���ABP�ա�ADQ���õ�AP=AQ����P��PM��AQ��M����AP��PM�����ǵõ�AQ��PM��˵���ڡ�APQ�У�AQ��AQ���ϵĸ߲���ȣ�ͬ���ɵ�AP���ϵĸ���AP����ȣ���Ϊ��APQΪ��г�����Σ�����PQ��PQ���ϵĸ���ȣ�����AC��PQ��E���ı���ABCD�������οɵá�BAC=��DAC���ɡ�ABP�ա�ADQ�á�BAP=��DAQ�����ݺ�г�����εĶ����з��̽�ý����
��� �⣺��1���Ǻ�г�����Σ�
�ʴ�Ϊ���ǣ�
��2����$\frac{AB}{BC}=\frac{{\sqrt{5}}}{2}$��
����AB=$\sqrt{5}x$��BC=2x��
��ͼ1������A��AD��BC��D��
��AB=AC��
��BD=CD=$\frac{1}{2}BC$=x��
�ߡ�ADB=90�㣬
��$AD=\sqrt{A{B^2}-B{D^2}}=2x$��
��AD=BC���ʡ�ABC�ǡ���г�����Ρ���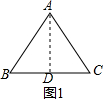
��3����������ã�PB=DQ=t��CP=CQ=3-t��
�ߡ�APQ�ǵȱ������Σ�
��AP=PQ��
��AB2+PB2=PC2+CQ2��
����32+t2=2��3-t��2�����t=6+3$\sqrt{3}$������������ȥ����t=$6-3\sqrt{3}$��
�൱t=6-3$\sqrt{3}$ʱ����APQΪ�ȱ������Σ�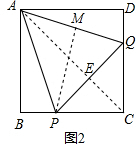
�ʴ�Ϊ��6-3$\sqrt{3}$��
���������BP=DQ=t cm��
���ı���ABCD�������Σ�
��AB=AD����ABP=��ADQ��
�ڡ�ABP���ADQ�У�$\left\{\begin{array}{l}{AB=AD}\\{��B=��D=90��}\\{PB=DQ}\end{array}\right.$��
���ABP�ա�ADQ��
��AP=AQ
����P��PM��AQ��M��
��AP��PM��
��AQ��PM
��˵���ڡ�APQ�У�AQ��AQ���ϵĸ߲���ȣ�
ͬ���ɵ�AP���ϵĸ���AP����ȣ�
��Ϊ��APQΪ��г�����Σ�
����PQ��PQ���ϵĸ���ȣ�
����AC��PQ��E
���ı���ABCD�������οɵá�BAC=��DAC��
�ɡ�ABP�ա�ADQ�á�BAP=��DAQ��
���PAC=��QAC��
��AP=AQ������AC��PQ��
��BP=DQ=t��
��CP=CQ=3-t��
��CE=$\frac{{\sqrt{2}}}{2}��{3-t}��$��PQ=$\sqrt{2}��{3-t}��$��
��AE=$3\sqrt{2}-\frac{{\sqrt{2}}}{2}��{3-t}��$��
��AE=PQ�ɵ�$3\sqrt{2}-\frac{{\sqrt{2}}}{2}��{3-t}��$=$\sqrt{2}��{3-t}��$���t=1��
��AE=PQ=2$\sqrt{2}$��
���г�����Ρ�APQ�����Բ�뾶Ϊr��
��r2-2=��2$\sqrt{2}$-r��2
��ã�r=$\frac{5}{4}$$\sqrt{2}$
���г�����Ρ�APQ�����Բ�뾶Ϊ$\frac{5}{4}\sqrt{2}$��
�ʴ�Ϊ��$\frac{4}{5}$$\sqrt{2}$��
���� ���⿼���˵���ֱ�������ε����ʣ�ȫ�������ε��ж������ʣ������ε����ʣ������ε����Բ�����ʣ����ɶ�������ȷ�������¶��塰��г�����Ρ��ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
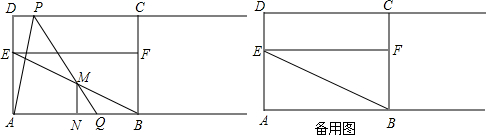
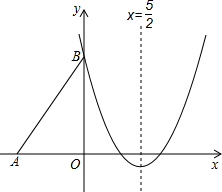 ��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=$\frac{2}{3}$x2+bx+c������B���Ҷ�����ֱ��x=$\frac{5}{2}$�ϣ�
��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=$\frac{2}{3}$x2+bx+c������B���Ҷ�����ֱ��x=$\frac{5}{2}$�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
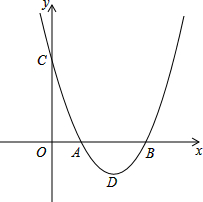 ��֪��������y=x2+bx+c��x�����������ֱ�ΪA��1��0����B��3��0������y�ύ�ڵ�C��
��֪��������y=x2+bx+c��x�����������ֱ�ΪA��1��0����B��3��0������y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2��a��1 | B�� | -3��a��-2 | C�� | -3��a��-2 | D�� | -3��a��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com