
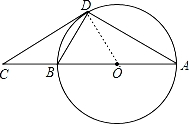
如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.
(1)求证:CD是⊙O的切线;
(2)若半径OB=2,求AD的长.

【考点】切线的判定;含30度角的直角三角形;勾股定理.
【专题】证明题.
【分析】(1)由于BO=BD=BC,即DB为△ODC的边OC的中线,且有DB=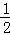 OC,则∠ODC=90°,然后根据切线的判定方法即可得到结论;
OC,则∠ODC=90°,然后根据切线的判定方法即可得到结论;
(2)由AB为⊙O的直径得∠BDA=90°,而BO=BD=2,则AB=2BD=4,然后根据勾股定理可计算出AD.
【解答】(1)证明:连结OD,如图,
∵BO=BD=BC,
∴BD为△ODC的中线,且DB=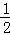 OC,
OC,
∴∠ODC=90°,
∴OD⊥CD,
而OD为⊙O的半径,
∴CD是⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠BDA=90°,
∵BO=BD=2,
∴AB=2BD=4,
∴AD=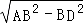 =2
=2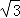 .
.
【点评】本题考查了切线的判定定理:过半径的外端点且与半径垂直的直线为圆的切线.也考查了直角三角形的判定方法、勾股定理.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )
A.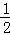 B.
B. C.
C.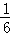 D.
D.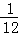
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )


A.m+3 B.m+6 C.2m+3 D.2m+6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com