
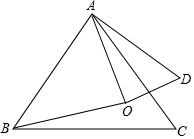
 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,分析 (1)根据旋转前后图形不发生变化,得出三角形COD是等边△OCD;
(2)根据等腰三角形的性质,分别假设AO=AD,OA=OD,OD=AD,从而求出α.
解答 解:(1)∵CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)∵∠AOC=360°-110°-α=250°-α,∠AOD=∠AOC-60°=190°-α,
∵∠ADC=∠BOC=α,
∴∠ODA=α-60°,
△AOD为等腰三角形,
当AO=OD时,∠AOD+2∠ODA=180°,
即190°-α+2×(α-60°)=180°,解得α=110°,
当AO=AD时,∠AOD=∠ODA,即190°-α=α-60°,解得α=125°,
当OD=AD时,2×(190°-α)+α-60°=180°,解得α=140°
所以当α为110°、125°、140°时,△AOD是等腰三角形.
点评 此题主要考查了等边三角形的性质与判定,以及等腰三角形的性质和旋转的性质等知识,根据旋转前后图形不变是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 中国古代对勾股定理有深刻的认识.
中国古代对勾股定理有深刻的认识.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
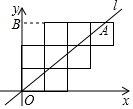 八个边长为1的正方形如图所示的位置摆放在平面直角坐标系中,经过原点的直线l将这八个正方形分成面积相等的两部分,则这条直线的解析式是y=$\frac{9}{10}$x.
八个边长为1的正方形如图所示的位置摆放在平面直角坐标系中,经过原点的直线l将这八个正方形分成面积相等的两部分,则这条直线的解析式是y=$\frac{9}{10}$x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com