Question

5．已知，O是直线AB上的一点，∠COD是直角，OE平分∠BOC．
（1）如图1，若∠AOC=40°，求∠D0E的度数；
（2）在图1中，若∠AOC=a，直接写出∠DOE的度数（用含a的代数式表示）；
（3）将图1中的∠DOC绕顶点O顺时针旋转至图2的位置．①探究∠AOC和∠DOE的度数之间的关系，写出你的结论，并说明理由；②在∠AOC的内部有一条射线OF，满足：2∠AOF+∠BOE=$\frac{1}{2}$（∠AOC-∠AOF），试确定∠AOF与∠DOE的度数之间的关系，说明理由．

Answer 1

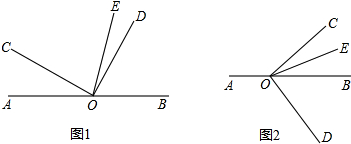
分析 （1）由∠AOC的度数可以求得∠BOC的度数，由OE平分∠BOC，可以求得∠COE的度数，又由∠DOC=90°可以求得∠DOE的度数；
（2）由第（1）问的求法，可以直接写出∠DOE的度数；
（3）①首先写出∠AOC和∠DOE的度数之间的关系，由∠COD是直角，OE平分∠BOC，BOC+∠AOC=180°，可以建立各个角之间的关系，从而可以得到∠AOC和∠DOE的度数之间的关系；
②首先得到∠AOF与∠DOE的度数之间的关系，由2∠AOF+∠BOE=$\frac{1}{2}$（∠AOC-∠AOF），∠COD是直角，OE平分∠BOC，∠AOC和∠DOE的关系，可以建立各个角之间的关系，从而可以得到∠AOF与∠DOE的度数之间的关系．

解答 解：（1）∵∠COD是直角，OE平分∠BOC，∠AOC=40°，
∴∠BOC=180°-∠AOC=140°，∠COE=$\frac{1}{2}∠BOC$，∠COD=90°．
∴∠COE=70°，∠DOE=∠COD-∠COE=90°-70°=20°．
即∠DOE=20°．
（2）∵∠COD是直角，OE平分∠BOC，∠AOC=a，
∴∠DOE=90°-$\frac{180°-a}{2}$=90°-90°+$\frac{a}{2}$=$\frac{a}{2}$．
即∠DOE=$\frac{a}{2}$．
（3）①∠AOC=2∠DOE．
理由：∵OE平分∠BOC，
∴∠BOC=2∠COE．
∵∠COD是直角，∠AOC+∠BOC=180°，
∴∠DOE+∠COE=90°，∠AOC+2∠COE=180°．
∴∠AOC+2（90°-∠DOE）=180°．
化简，得∠AOC=2∠DOE．
②2∠DOE-$\frac{5}{2}∠AOF=90°$．
理由：∵2∠AOF+∠BOE=$\frac{1}{2}$（∠AOC-∠AOF），∠AOC=2∠DOE，
∴2∠AOF+∠BOE=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠AOF．
即$\frac{5}{2}∠AOF=∠DOE-∠BOE$．
∴$\frac{5}{2}∠AOF=∠DOB$．
∵∠DOB+∠BOC=90°，∠AOC+∠BOC=180°，∠AOC=2∠DOE．
∴$\frac{5}{2}∠AOF+180°-∠AOC=90°$．
∴$\frac{5}{2}∠AOF+180°-2∠DOE=90°$．
化简，得2∠DOE-$\frac{5}{2}∠AOF=90°$．

点评 本题考查角的计算、角平分线的性质，解题的关键是根据题目中的信息，建立各个角之间的关系，然后找出所求问题需要的条件．