
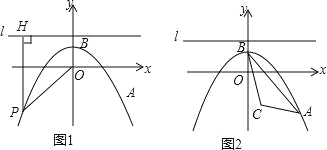
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
(1)求抛物线的解析式,并写出其顶点B的坐标;
(2)①当P点运动到A点处时,计算:PO= ,PH= ,由此发现,PO PH(填“>”、“<”或“=”);
②当P点在抛物线上运动时,猜想PO与PH有什么数量关系,并证明你的猜想;
(3)如图2,设点C(1,﹣2),问是否存在点P,使得以P,O,H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为y=﹣![]() x2+1,顶点B(0,1);(2)①5,5,=;②结论:PO=PH,理由详见解析;(3)点P坐标(1,
x2+1,顶点B(0,1);(2)①5,5,=;②结论:PO=PH,理由详见解析;(3)点P坐标(1,![]() )或(﹣1,
)或(﹣1,![]() ).
).
【解析】
试题分析:(1)把A点的坐标代入y=ax2+1求得a值,即可得函数解析式,根据解析式确定顶点坐标即可;(2)①求出PO、PH即可得结论;②结论:PO=PH.设点P坐标(m,﹣![]() m2+1),根据两点之间距离公式分别求得PH、PO长,即可得结论.(3)首先判断PH与BC,PO与AC是对应边,设点P(m,﹣
m2+1),根据两点之间距离公式分别求得PH、PO长,即可得结论.(3)首先判断PH与BC,PO与AC是对应边,设点P(m,﹣![]() m2+1),由
m2+1),由![]() 列出方程即可解决问题.
列出方程即可解决问题.
试题解析:(1)解:∵抛物线y=ax2+1经过点A(4,﹣3),
∴﹣3=16a+1,
∴a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() x2+1,顶点B(0,1).
x2+1,顶点B(0,1).
(2)①当P点运动到A点处时,∵PO=5,PH=5,
∴PO=PH,
②结论:PO=PH.
理由:设点P坐标(m,﹣![]() m2+1),
m2+1),
∵PH=2﹣(﹣![]() m2+1)=
m2+1)=![]() m2+1
m2+1
PO=![]() =
=![]() m2+1,
m2+1,
∴PO=PH.
(3)∵BC=![]() ,AC=
,AC=![]() ,AB=
,AB=![]() ,
,
∴BC=AC,
∵PO=PH,
又∵以P,O,H为顶点的三角形与△ABC相似,
∴PH与BC,PO与AC是对应边,
∴![]() ,设点P(m,﹣
,设点P(m,﹣![]() m2+1),
m2+1),
∴ ,
,
解得m=±1,
∴点P坐标(1,![]() )或(﹣1,
)或(﹣1,![]() ).
).


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
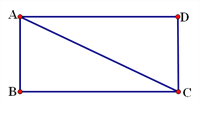
【题目】如图,有一个长方形花园,对角线AC是一条小路,现要在AD边上找一个位置建报亭,使报亭到小路两端点A、C的距离相等.
(1)用尺规作图的方法,在图中找出报亭位置(不写作法,但需保留作图痕迹,交代作图结果);
(2)如果AD=80m,CD=40m,求报亭到小路端点A的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
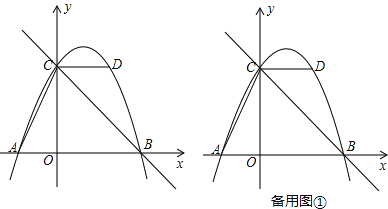
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
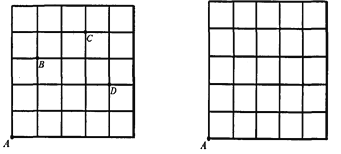
【题目】在边长为1的小正方形组成的网格中,把一个点先沿水平方向平移|a|格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移|b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的点,我们把这个过程记为(a,b).
例如,从A到B记为:A→B(+l,+3);从C到D记为:C→D(+1,-2),
回答下列问题:
(1)如图1,若点A的运动路线为:A→B→C→A,请计算点A运动过的总路程.
(2)若点A运动的路线依次为:A→M(+2,+3),M→N(+1,-1),N→P(-2,+2),P→Q(+4,-4).请你依次在图2上标出点M、N、P、Q的位置.
(3)在图2中,若点A经过(m,n)得到点E,点E再经过(p,q)后得到Q,则m与p满足的数量关系是 ;n与q满足的数量关系是 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com