
【题目】若有理数 a,b 满足![]() ,则a=____, b=____.
,则a=____, b=____.
【答案】(m-2,n+2)或(m-6,n-5) ![]()
【解析】
根据等式分两种情况讨论即可;
①分A点平移到y轴上、B点平移到x轴上和A点平移到x轴上、B点平移到y轴上两种情况讨论即可.
②根据CD∥AB,得到∠B=∠DCE,∠A+∠ADC=![]() ,再根据CF平分∠DCE,DG平分∠ADC,得到∠DCF=
,再根据CF平分∠DCE,DG平分∠ADC,得到∠DCF=![]() ∠B,∠CDG=
∠B,∠CDG=![]() ,又因为D、G、F在同一条直线上,所以∠CDG=∠F+∠DCF,
,又因为D、G、F在同一条直线上,所以∠CDG=∠F+∠DCF,![]() ,最后根据∠A+∠B=3∠F即可求解.
,最后根据∠A+∠B=3∠F即可求解.
解:∵![]()
∴![]()
当![]() =
=![]() 时
时
![]()
![]()
![]()
当![]() 时
时
![]()
![]()
![]()
①第一种情况:AB先向左平移2个单位,再向上平移2个单位.
则平移后点 P 的坐标为(m-2,n+2)
第二种情况:AB先向下平移5个单位,再向左平移6个单位.
则平移后点 P 的坐标为(m-6,n-5).
②∵CD∥AB
∴∠B=∠DCE,∠A+∠ADC=![]()
∵CF平分∠DCE,DG平分∠ADC
∴∠DCF=![]() ∠B,∠CDG=
∠B,∠CDG=![]()
∵F在GD的延长线上
∴D、G、F在同一条直线上
∴∠CDG是![]() 的外角
的外角
∴∠CDG=∠F+∠DCF
∴![]()
∵∠A+∠B=3∠F
∴![]()
∠F=![]()


科目:初中数学 来源: 题型:
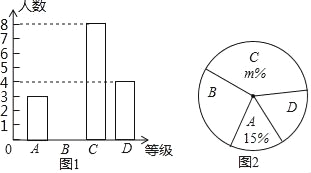
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为 ,表示“D等级”的扇形的圆心角为 度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,DE为△ABC的中位线,点F为DE上一点,且∠AFB=90°,若AB=8,BC=10,则EF的长为 .
B.小智同学在距大雁塔塔底水平距离为138米处,看塔顶的仰角为24.8(不考虑身高因素),则大雁塔市约为米.(结果精确到0.1米)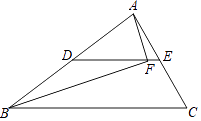
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF,延长DA交FG于点H,则GH的长为( )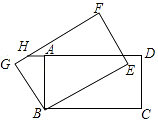
A.8﹣4 ![]()
B.![]() ﹣4
﹣4
C.3 ![]() ﹣4
﹣4
D.6﹣3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°, 试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式, 将答案按序号填在答题卷的对应位置内)
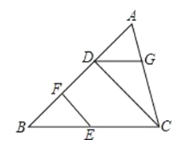
证明:∵CD⊥AB,EF⊥AB( ① )
∴∠BFE=∠BDC=90°( ② )
∴EF∥CD( ③ )
∴∠BEF= ④ ( ⑤ )
又∵∠B+∠BDG=180°( ⑥ )
∴BC∥DG( ⑦ )
∴∠CDG= ⑧ ( ⑨ )
∴∠CDG=∠BEF( ⑩ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )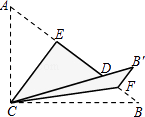
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com