
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )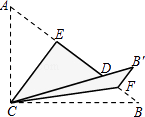
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:根据折叠的性质可知CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,
∴B′D=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC= ![]() ACBC=
ACBC= ![]() ABCE,
ABCE,
∴ACBC=ABCE,
∵根据勾股定理求得AB=5,
∴CE= ![]() ,
,
∴EF= ![]() ,ED=AE=
,ED=AE= ![]() =
= ![]() ,
,
∴DF=EF﹣ED= ![]() ,
,
∴B′F= ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() .
.
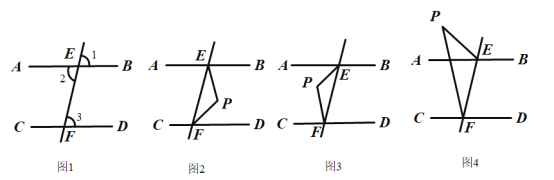
(1)如图1,若![]() ,求
,求![]() ,
,![]() 的度数;
的度数;
(2)若点![]() 是平面内的一个动点,连接
是平面内的一个动点,连接![]() 、
、![]() ,探索
,探索![]() 、
、![]() 、
、![]() 之间的数量关系;
之间的数量关系;
①当点![]() 在图2的位置时,请写出
在图2的位置时,请写出![]() 、
、![]() 、
、![]() 之间的数量关系并证明;
之间的数量关系并证明;
②当点![]() 在图3的位置时,请写出
在图3的位置时,请写出![]() 、
、![]() 、
、![]() 之间的数量关系并证明;
之间的数量关系并证明;
③当点![]() 在图4的位置时,请直接写出
在图4的位置时,请直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1 ,
其中正确的是( )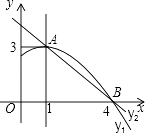
A.①②③
B.①③④
C.①③⑤
D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
请根据图表信息解答下列问题: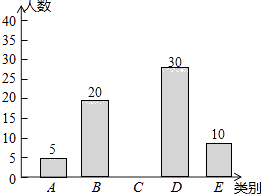
(1)a=;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC= ![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;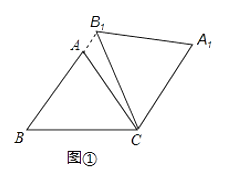
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.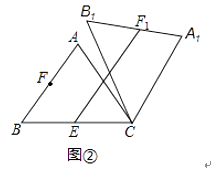
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() .在边
.在边![]() 上取一点
上取一点![]() ,以
,以![]() 为顶点、
为顶点、![]() 为一条边作
为一条边作![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() .
.
(1)如图(1),当点![]() 在边
在边![]() 上时,请说明①
上时,请说明①![]() ;②
;②![]() 成立的理由.
成立的理由.
(2)如图(2),当点![]() 在
在![]() 的延长线上时,试判断
的延长线上时,试判断![]() 与
与![]() 是否相等?
是否相等?

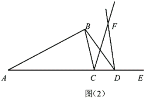
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com