练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如果两圆的半径长分别为1和3，圆心距为3，那么这两个圆的位置关系是（　　）
    A．内含B．内切C．外切D．相交

    分析 由两圆的半径长分别为1和3，圆心距为3，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．

    解答 解：∵两圆的半径长分别为1和3，
    ∴两圆的半径和为4，差为2，
    ∵圆心距为3，
    ∴这两个圆的位置关系是：相交．
    故选D．

    点评 此题考查了圆与圆的位置关系．注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．如图，正方形ABCD中，点E，F分别在BC，CD上，△AEF是等边三角形，连接AC交EF于点G，下列结论：①CE=CF，②∠AEB=75°，③AG=2GC，④BE+DF=EF，⑤S△CEF=2S△ABE，其中结论正确的个数为（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

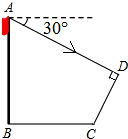    18．小明准备测量学校旗杆的高度，他发现斜坡正对着太阳时，旗杆AB影子恰好落在水平地面BC和斜坡面CD上，测得旗杆在水平地面上的影长BC=20m，在斜坡坡面上的影长
    CD=8m，太阳光线AD与水平地面成30°角，且太阳光线AD与斜坡坡面互相垂直，请你帮小明求出旗杆AB的高度（结果保根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在△ABC中，∠ACB=90°，CD⊥AB于点D．
    （1）如图（1），AC=BC，点E，F分别在AC，BC上，∠EDF=90°，则DE与DF的数量关系为DE=DF．
    （2）如图（2），AC=BC，延长BC到点F，沿CA方向平移线段CF到EG，且点G在边BA的延长线上，求证：DE=DF，DE⊥DF；
    （3）如图（3），∠B=30°，延长BC到点F，沿CA方向平移线段CF到EG，且点G在边BA的延长线上，直接写出线段DE与DF的位置关系和数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．图1是一个长为a，宽为b的长方形，图2是一个长为（a+b），宽为（a-b）的长方形，图3是由4个如图1中的长方形拼成的一个大正方形，若图1中的长方形周长数等于图2中长方形的面积数，图2中长方形的面积是图3中阴影部分的面积的5倍，则（2a-5b）2的值为64．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．从1至9这9个自然数中任取一个数，是素数的概率是$\frac{4}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．化简求值：$\frac{1}{x-2}•\frac{{x}^{2}-4}{x}-\frac{1+x}{{x}^{2}+x}$，其中x=$\sqrt{2}-1$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．化简：$a+b-\frac{{{a^2}-{b^2}}}{a-b}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．函数y=$\frac{x-1}{4x}$的定义域是x≠0．

    查看答案和解析>>

    同步练习册答案