
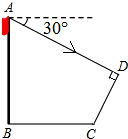
 小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长
小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长分析 设AD与BC的延长线交于E,在Rt△CDE中,由含30°角的直角三角形的性质求出CE=16m,得出BE,再由三角函数求出AB即可.
解答 解:作AD与BC的延长线,交于E点.如图所示:
根据平行线的性质得:∠E=30°,
∴CE=2CD=2×8=16.
则BE=BC+CE=20+16=36.
在直角△ABE中,tan∠E=$\frac{AB}{BE}$,
∴AB=BE•tan30°=36×$\frac{\sqrt{3}}{3}$=12$\sqrt{3}$(m).
即旗杆AB的高度是12$\sqrt{3}$m.
点评 此题考查了解直角三角形的应用、含30°角的直角三角形的性质;由含30°角的直角三角形的性质求出CE,得出BE是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
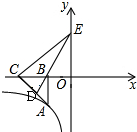 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
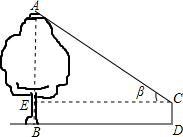 小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图),为测量此时风筝的高度,他俩按如下步骤操作:
小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图),为测量此时风筝的高度,他俩按如下步骤操作:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com