
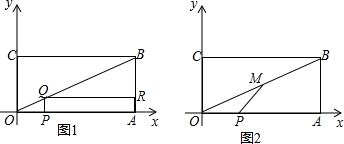
分析 (1)由四边形OABC为矩形,PQ⊥OA,可得$\frac{PQ}{AB}=\frac{OP}{OA}$,继而求得PQ的值,则可求得S与x之间的函数关系式.
(2)由(1),利用二次函数的最值,即可求得答案;
(3)分别从当OM为等腰△POM底边,当PM为等腰△POM底边与当OP为等腰△POM底边,去分析求解即可求得答案.
解答 解:(1)∵点A、B的坐标分别为(4,0)、(4,3),
∴OA=4,AB=3,
∴PA=OA-OP=4-x,
∵四边形OABC为矩形,PQ⊥OA,
∴PQ∥AB,
∴$\frac{PQ}{AB}=\frac{OP}{OA}$,
∴PQ=$\frac{3x}{4}$,
∴S=$\frac{3}{4}$x•(4-x)=-$\frac{3}{4}$x2+3x;
(2)∵S=-$\frac{3}{4}$x2+3x=-$\frac{3}{4}$(x2-4x)=-$\frac{3}{4}$(x-2)2+3,
∴当x=2时,四边形PQRA的面积最大;
(3)如图a,当OM为等腰△POM底边时,过点P作PN⊥OB于点N,则ON=MN,
∵∠NOP=∠AOB,∠ONP=∠OAB=90°,
∴△OPN∽△OBA,
∴ON:OA=OP:OB,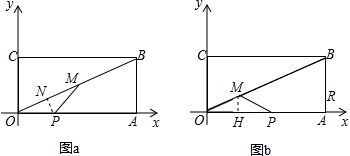
∴ON:4=t:5,
解得:ON=$\frac{4}{5}$t,
∵OM=OB-BM=5-2t,
∴5-2t=2×$\frac{4t}{5}$,
解得:t=$\frac{25}{18}$;
当PM为等腰△OPM底边时,则OP=OM,
即t=5-2t,
解得:t=$\frac{5}{3}$;
如图b,若OP为等腰△OPM底边时,过点M作MH⊥OA于点H,则OP=2OH,
∵MH∥AB,
∴△OHM∽△OAB,
∴OM:OB=OH:OA,
∴$\frac{5-2t}{5}$=$\frac{OH}{4}$,
∴OH=$\frac{20-8t}{5}$,
∴t=2×$\frac{20-8t}{5}$,
解得:t=$\frac{40}{21}$;
综上所述:当t=$\frac{25}{18}$或$\frac{5}{3}$或$\frac{40}{21}$时,△OPM为等腰三角形.
点评 此题属于相似三角形的综合题.考查了相似三角形的判定与性质、二次函数的性质以及等腰三角形的性质.注意方程思想与分类讨论思想的应用是解此题的关键.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
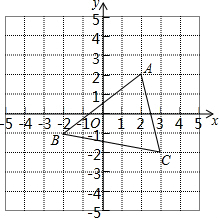 如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.
如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
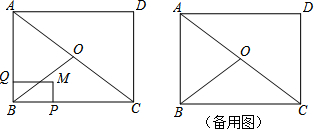
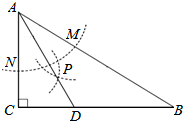 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
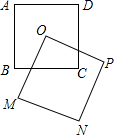 如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.
如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com