
【题目】在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, ![]() m)(m为非负数),则CA+CB的最小值是( ).
m)(m为非负数),则CA+CB的最小值是( ).
A.6
B.![]()
C.![]()
D.5
【答案】C
【解析】解答:如图所示:
∵点C的坐标为(m, ![]() m)(m为非负数),
m)(m为非负数),
∴点C的坐标所在直线为y= ![]() x,
x,
点A关于直线y= ![]() x的对称点的坐标为A′,则AA′所在直线为y=
x的对称点的坐标为A′,则AA′所在直线为y= ![]() x+b,
x+b,
把点A的坐标( 2,0 )代入得 ![]() ×2+b=0,
×2+b=0,
解得b= ![]() .
.
故AA′所在直线为y= ![]() x+
x+ ![]() .
.
联立C的坐标所在直线和AA′所在直线可得 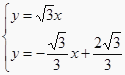 ,
,
解得 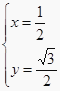 ,
,
∴C的坐标所在直线和AA′所在直线的交点M的坐标为( ![]() ,
, ![]() ),
),
∴点A关于直线y= ![]() x的对称点的坐标为(-1,
x的对称点的坐标为(-1, ![]() ),
),
∴A′B= ![]() =
= ![]() =2
=2 ![]() ,即CA+CB的最小值.
,即CA+CB的最小值.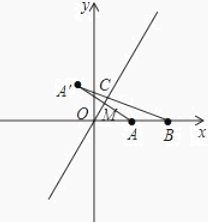
故选C.
分析:分别得到点C的坐标所在直线,点A关于点C的坐标所在直线的对称点的坐标A′所在直线AA′的解析式,求得两条直线的交点,进一步得到A′点的坐标,再根据两点间的距离公式即可求解.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对轴对称-最短路线问题的理解,了解已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.
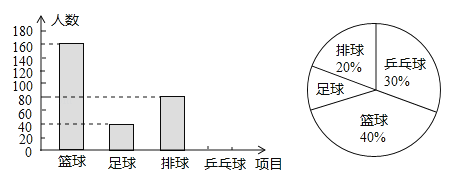
请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接一个四边形各边的中点,得到一个矩形,则原四边形一定是( )
A. 菱形 B. 矩形 C. 对角线相等的四边形 D. 对角线垂直的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡把果树林分为两部分,左地块用新技术管理,右地块用老方法管理,管理成本相同,她在左、右两地块上各随机选取20棵果树,按产品分成甲、乙、丙、丁四个等级(数据分组包括左端点不包括右端点),并制作如下两幅不完整的统计图:

(1)补齐左地块统计图,求右地块乙级所对应的圆心角的度数;
(2)比较两地块的产量水平,并说明试验结果;
(3)在左地块随机抽查一棵果树,求该果树产量为乙级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AB=4 ![]() ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ).
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ). 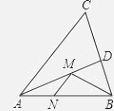
A.3
B.4
C.5
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com