
【题目】如图,平行四边形硬纸片ABCD中,![]() ,
,![]() ,
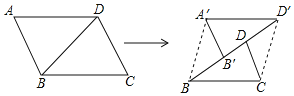
,![]() ,沿着对角线BD将平行四边形剪开成两个三角形,固定
,沿着对角线BD将平行四边形剪开成两个三角形,固定![]() 不动,将
不动,将![]() 沿射线BD方向以每秒1个单位的速度匀速运动
沿射线BD方向以每秒1个单位的速度匀速运动![]() 运动后
运动后![]() 记为
记为![]() 连接
连接![]() 和
和![]() .
.
![]() 小明认为在运动过程中,始终有
小明认为在运动过程中,始终有![]() ,你同意吗?请说明理由.
,你同意吗?请说明理由.
![]() 保持上述条件不变,当
保持上述条件不变,当![]() 运动______秒时,四边形
运动______秒时,四边形![]() 为菱形.
为菱形.
![]() 保持上述条件不变,当
保持上述条件不变,当![]() 运动______秒时,四边形
运动______秒时,四边形![]() 为矩形.
为矩形.
【答案】![]() 同意,(2)4;(3)
同意,(2)4;(3)![]() .
.
【解析】
(1)根据平行四边形的性质得到AD=BC,AD//BC,∠ABD=∠CDB,根据平移的性质、全等三角形的判定定理得到△A'BB'≌△CD'D,根据全等三角形的性质证明;
(2)根据勾股定理的逆定理得到∠ABD=90°,根据菱形的性质、勾股定理计算即可;
(3)根据矩形的性质得到∠BA'D'=90°,证明△A'BB'∽△D'A'B',根据相似三角形的性质列出比例式,计算即可.
![]() 同意,理由如下:
同意,理由如下:
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]() ,
,![]() ,
,![]() ,
,
由平移的性质可知,![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
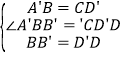 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 始终有
始终有![]() ;
;
![]() ,
,
![]() ,
,
当四边形![]() 为菱形时,
为菱形时,![]() ,
,
在![]() 中,
中,![]() ,
,
故答案为:4;
![]() 当四边形
当四边形![]() 为矩形时,
为矩形时,![]() ,又
,又![]() ,
,
![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,![]() ,
,
故答案为:![]() .
.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB= ![]() ,BC=
,BC= ![]() .
.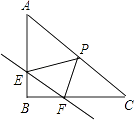
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为![]() BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
![]()
A. 点E B. 点F C. 点M D. 点N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点. 
(1)直接写出ED和EC的数量关系:;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,E、F分别是边BC、CD的中点,连接AE,AF.
(1)如图1,若四边形ABCD的面积为5,则四边形AECF的面积为____________;
(2)如图2,延长AE至G,使EG=AE,延长AF至H,使FH=AF,连接BG、GH、HD、DB.
求证:四边形BGHD是平行四边形;
(3)如图3,对角线 AC、BD相交于点M, AE与BD交于点P, AF与BD交于点N. 直接写出BP、PM、MN、ND的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com