
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想; 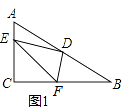
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明) 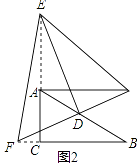
【答案】
(1)结论:AE2+BF2=EF2.
理由:如图1中,延长FD到M,使得DM=DF,连接AM,EM.
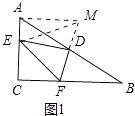
在△ADM和△BDF中,
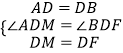 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2,
∴AE2+BF2=EF2.
(2)如图2中,结论不变.AE2+BF2=EF2
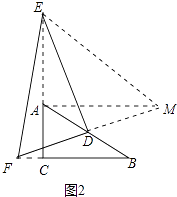
理由:延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
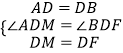 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=∠CAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2,
∴AE2+BF2=EF2.
【解析】(1)结论:AE2+BF2=EF2 . 如图1中,延长FD到M,使得DM=DF,连接AM,EM.首先证明△ADM≌△BDF,得到AM=FB,再证明△AEM是直角三角形,理由勾股定理即可解决问题.(2)结论不变,证明方法类似.
【考点精析】关于本题考查的直角三角形斜边上的中线,需要了解直角三角形斜边上的中线等于斜边的一半才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】荔枝是岭南一带的特色时令水果.今年5月份荔枝一上市,某水果店的老板用3000元购进了一批荔枝,由于荔枝刚在果园采摘比较新鲜,前两天他以高于进价40% 的价格共卖出150千克,由于荔枝保鲜期短,第三天他发现店里的荔枝卖相已不大好,于是果断地将剩余荔枝以低于进价20%的价格全部售出,前后一共获利750元.
(1)若购进的荔枝为![]() 千克,则这批荔枝的进货价为 ;(用含
千克,则这批荔枝的进货价为 ;(用含![]() 的式子来表示)
的式子来表示)
(2)求该水果店的老板这次购进荔枝多少千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为___________cm

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M , 交y轴于点N , 再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P . 若点P的坐标为(2a , b+1),则a与b的数量关系为( ) 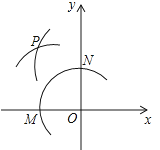
A.a-b
B.2a+b=-1
C.2a-b=l
D.2a+b=l
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠C=α,∠EAC+∠FBC=β 
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是 . (用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1 , ∠EAP1与∠FBP1的平分线交于P2;依此类推,则∠P5= . (用α、β表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com