
| A. | 136° | B. | 34° | C. | 168° | D. | 124° |
分析 首先根据三角形内角和定理求得∠ABC+∠ACB,然后根据内心的定义证明∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),然后根据三角形内角和定理求解.
解答 解:在△ABC中,∠ABC+∠ACB=180°-∠BAC=180°-68°=112°,
∵点P是△ABC的内心,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×112=56°,
∴∠BOC=180°-(∠OBC+∠OCB)=180-56=124°.
故选D.
点评 此题主要考查了三角形的内心的计算,正确理解∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)是关键.


科目:初中数学 来源: 题型:解答题
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
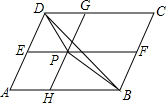 如图,点P为平行四边形ABCD内一点,过P点分别作AB、AD的平行线,交平行四边形ABCD的各边于点E、F、G、H.已知四边形AHPE的面积为3,四边形PFCG的面积为5,则△BDP的面积是1.
如图,点P为平行四边形ABCD内一点,过P点分别作AB、AD的平行线,交平行四边形ABCD的各边于点E、F、G、H.已知四边形AHPE的面积为3,四边形PFCG的面积为5,则△BDP的面积是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
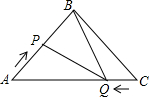 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com