
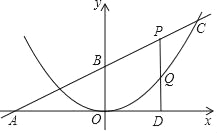
����Ŀ����ͼ��ֱ��y=kx+b�������ύ��A��B���㣬���е�B������Ϊ��0��4����tan��BAO=![]() ��һ�������ߵĶ���Ϊ����ԭ�㣬����ֱ��y=kx+b���ڵ�C��m��8������PΪ�߶�BC��һ���㣨�����B����C�غϣ���PD��x���ڵ�D�����������ڵ�Q.
��һ�������ߵĶ���Ϊ����ԭ�㣬����ֱ��y=kx+b���ڵ�C��m��8������PΪ�߶�BC��һ���㣨�����B����C�غϣ���PD��x���ڵ�D�����������ڵ�Q.
��1����ֱ�ߺ������ߵĺ�����ϵʽ��
��2�����P�ĺ�����Ϊt���߶�PQ�ij���Ϊd�����d��t֮��ĺ�����ϵʽ�������d�����ֵ��
��3���Ƿ���ڵ�P��λ�ã�ʹ���Ե�P��D��BΪ������������ǵ��������Σ�������ڣ�ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x+4��y=
x+4��y=![]() x2����2��d=��
x2����2��d=��![]() t2+
t2+![]() t+4,��t=2ʱ��d�����ֵ
t+4,��t=2ʱ��d�����ֵ![]() ����3�����ڣ�P������Ϊ��2+2
����3�����ڣ�P������Ϊ��2+2![]() ��5+
��5+![]() ����
����![]() ��
��![]() �������ɼ�����
�������ɼ�����
����������1�����������κ��������A�����꣬�����ô���ϵ����������������ߵĽ���ʽ��
��2������P��Q�������ú�t��ʽ�ӱ�ʾ���������������ľ��빫ʽ�������d��t֮��ĺ�����ϵʽ�����ö��㹫ʽ�������d�����ֵ��
��3����PB=BD��PB=PD��BD=PD��������������ۼ���.
�⣺��1����B��0��4����
��OB=4��
��Rt��AOB����tan��BAO=![]() =
=![]() ��
��
��OA=2OB=8��
��A����8��0����
��A����8��0����B��0��4������y=kx+b��![]() �����
����� ��
��
��ֱ��AB�Ľ���ʽΪy=![]() x+4��
x+4��
��y=8ʱ��![]() x+4=8�����x=8����C��8��8����
x+4=8�����x=8����C��8��8����
�������߽���ʽΪy=ax2��
��C��8��8�������64a=8�����a=![]() ��
��
�������ߵĽ���ʽΪy=![]() x2��
x2��
��2����P��t��![]() t+4����0��t��8������Q��t��
t+4����0��t��8������Q��t��![]() t2����
t2����
��d=![]() t+4��
t+4��![]() t2
t2
=��![]() t2+
t2+![]() t+4��
t+4��
��d=��![]() ��t��2��2+
��t��2��2+![]() ��
��
�൱t=2ʱ��d�����ֵ![]() ��
��
��3�����ڣ�
��B��0��4����P��t��![]() t+4����D��t��0����
t+4����D��t��0����
��PB2=t2+��![]() t+4��4��2=
t+4��4��2=![]() t2��DB2=t2+42=t2+16��PD2=��
t2��DB2=t2+42=t2+16��PD2=��![]() t+4��2=
t+4��2=![]() t2+4t+16��
t2+4t+16��
��PB=BDʱ����PBDΪ���������Σ���![]() t2=t2+16�����t1=8����ȥ����t2=��8����ȥ����
t2=t2+16�����t1=8����ȥ����t2=��8����ȥ����
��PB=PDʱ����PBDΪ���������Σ���![]() t2=
t2=![]() t2+4t+16�����t1=2��2
t2+4t+16�����t1=2��2![]() ����ȥ����t2=2+2
����ȥ����t2=2+2![]() ����ʱP������Ϊ��2+2
����ʱP������Ϊ��2+2![]() ��5+
��5+![]() ����
����
��BD=PDʱ����PBDΪ���������Σ���t2+16=![]() t2+4t+16�����t1=0����ȥ����t2=
t2+4t+16�����t1=0����ȥ����t2=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��
��![]() ����
����
����������P��������2+2![]() ��5+
��5+![]() ����
����![]() ��
��![]() ����
����


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������˹������Ϸ�У�ͼ��![]() ����ƽ��ʹ�����λ������ȷ��ƽ�Ʒ�ʽ�ǣ� ��
����ƽ��ʹ�����λ������ȷ��ƽ�Ʒ�ʽ�ǣ� ��
[Failed to download image : http://192.168.0.10:8086/QBM/2019/8/9/2265110730670080/2266396395864065/STEM/34cd169bb880437797498d7a59a34864.png]
A.������ƽ��5��������ƽ��3��
B.������ƽ��4��������ƽ��5��
C.������ƽ��4��������ƽ��4��
D.������ƽ��3��������ƽ��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������![]() �����������λ����ͼ��
�����������λ����ͼ��![]() Ϊ������
Ϊ������![]() ��һ�㣬
��һ�㣬![]() ������Ϊ
������Ϊ![]()
��1��ƽ��������![]() ��ʹ
��ʹ![]() ����ԭ���غϣ��뻭��ƽ�ƺ��������
����ԭ���غϣ��뻭��ƽ�ƺ��������![]()
��2��ֱ��д��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() �����ꣻ��д��ƽ�ƵĹ���.
�����ꣻ��д��ƽ�ƵĹ���.
![]() �� �� ����
�� �� ����
![]() �� �� ����
�� �� ����
![]() �� �� ����
�� �� ����
��3����������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ѧҪΪѧУ�Ƽ��С���ṩʵ�����ģ��ƻ�����A�͡�B�������ͺŵķŴ�������8��A�ͷŴ�5��B�ͷŴ�����220Ԫ��������4��A�ͷŴ�6��B�ͷŴ�����152Ԫ��
��1����ÿ��A�ͷŴ�ÿ��B�ͷŴ�����Ԫ��
��2����ƽ��ѧ��������A�ͷŴ�B�ͷŴ�75�����ܷ��ò�����1180Ԫ����ô�����Թ�����ٸ�A�ͷŴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
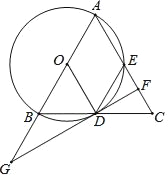
����Ŀ����ͼ����ABC�У�AB=AC����ABΪֱ���ġ�O��BC��AC��D��E���㣬����D����O�����ߣ���AC�ڵ�F����AB���ӳ����ڵ�G��
��1����֤��EF=CF��
��2����cos��ABC=![]() ��AB=10�����߶�AF�ij���
��AB=10�����߶�AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ι�˾�ھ�����������50���۹���ο�����ʹ�ã��ٶ�ÿ���۹һ�������ֻ�ܳ���һ�Σ���ÿ�����������x��Ԫ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=������������ѣ�
��2����ÿ�����������Ϊ����Ԫʱ��ÿ��ľ�������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӽҵ�ѧУ��ѧ����;�辭������·�ڣ�ÿ��·�ڶ����к졢��������ɫ���źŵƣ����źŵ���������£�
��1��������״ͼ�о�С��������ͨ�źŵƵ����������
��2��С������������ɫ�źŵĸ����ж��
��3��С������ɫ�����źŶ������ĸ����ж��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�����⣺̽������y=-![]() +|x|��ͼ�������ʣ�
+|x|��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���y=-![]() +|x|��ͼ�������ʽ�����̽����
+|x|��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=-![]() +|x|���Ա���x��ȡֵ��Χ�� ��
+|x|���Ա���x��ȡֵ��Χ�� ��
��2������y��x�ļ����Ӧֵ.
x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | �� |
y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | �� |
��ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��

��3���۲�ͼ��������Сֵ�� ��
��4����һ��̽������Ϻ�����ͼ��д���ú�����һ�����ʣ�������Сֵ���⣩�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ3x��6�Ľⶼ��ʹ����x��һ�β���ʽ��m-1��x��m+5��������ʹ����x�ķ�ʽ����![]() =
=![]() �������⣬��ô������������������m��ֵ֮����______��
�������⣬��ô������������������m��ֵ֮����______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com