
分析 首先建立直角坐标系,顶点为(4,3.2),起点为(0,0).设抛物线的解析式为y=a(x-4)2+3.2,求出a的值.再代入x的值后易求出y的值.
解答 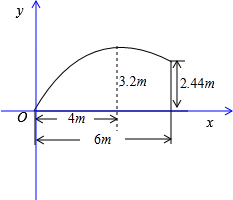 解:如图,建立直角坐标系,
解:如图,建立直角坐标系,
球飞行的路线为抛物线,顶点(4,3.2),起点(0,0),
设抛物线的解析式为y=a(x-4)2+3.2,
∴0=a(0-4)2+3.2,
∴a=-$\frac{1}{5}$;
∴抛物线的解析式为y=-$\frac{1}{5}$(x-4)2+3.2,
当x=6时,y=2.4<2.44,
故运动员这一脚能射中球门.
点评 本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
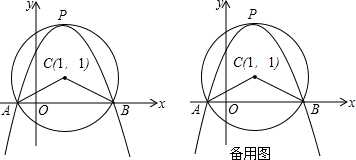
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
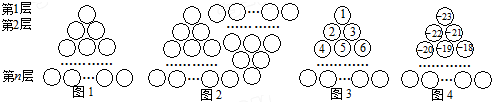
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=ax2+bx+c | B. | $y=\sqrt{{x^2}-1}$ | C. | $y=\frac{1}{x^2}$ | D. | $y=\frac{1}{8}{x^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | $\frac{1}{80}$ | D. | $\frac{1}{512}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2400÷70% | B. | 2400×70% | C. | 2400×(1-70%) | D. | 2400×7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6$\sqrt{2}$×$\sqrt{3}=6$$\sqrt{6}$ | B. | $\sqrt{8}$$÷\sqrt{2}=2$ | C. | $\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$ | D. | $\sqrt{8}-\sqrt{2}=2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com