
����Ŀ����ͼ��ͼ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���ABC�ڷ���ֽ�е�λ����ͼ��ʾ��
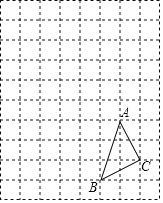
��1������ͼ�н���ƽ��ֱ������ϵ��ʹ��A��B���������ֱ�ΪA��2����1����B��1����4������д��C�����ꣻ
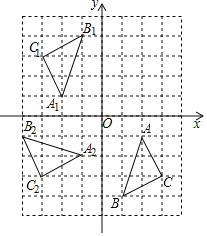
��2����ͼ��������ABC������ԭ����ת180�������A1B1C1����д��A1��B1��C1�����ꣻ
��3����ͼ��������ABC������ԭ��˳ʱ����ת90�������A2B2C2����д��A2��B2��C2�����꣮
���𰸡���1��ͼ�μ�������C��3����3������2��ͼ�μ�������A1����2��1����B1����1��4����C1����3��3������3��ͼ�μ�������A2����1����2����B2����4����1����C2����3����3��
��������
��1��������֪������꣬��������ϵ��������ϵȷ��C�����ꣻ
��2���ɹ���ԭ�����ĶԳ��Ի���A1B1C1����ȷ��д��A1��B1��C1�����ꣻ
��3����������ṹ�ҳ���A��B��C�Ƶ�O˳ʱ����ת90��Ķ�Ӧ��A2��B2��C2��λ�ã�����A2B2C2����ȷ��д��A2��B2��C2������.
�⣺��1������ϵ��ͼ��ʾ��C��3����3����
��2����A1B1C1��ͼ��ʾ��A1����2��1����B1����1��4����C1����3��3����
��3����A2B2C2��ͼ��ʾ��A2����1����2����B2����4����1����C2����3����3��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=��x+7a+1��ֱ��y=2x��2a+4ͬʱ������P����Q����M��0����1��ΪԲ�ģ�MOΪ�뾶��Բ�ϵ�һ�����㣬���߶�PQ����СֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AC=BC����C=90����AD����ABC�Ľ�ƽ���ߣ�DE��AB������ΪE��

��1����֪CD=4cm����AC�ij���
��2����֤��AB=AC+CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
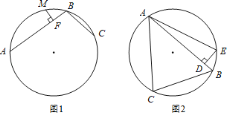
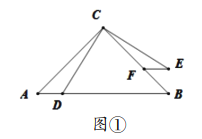
����Ŀ�����壺Բ���й����˵����������ɵ����߳�ΪԲ��һ�����ң����������Ҷ�������ͼ1��AB��BC���Բ�����ң�AB��BC��M�ǻ�ABC���е㣬MF��AB��F����AF��FB+BC��
��ͼ2����ABC�У���ABC��60�㣬AB��8��BC��6��D��AB��һ�㣬BD��1����DE��AB����ABC�����Բ��E������EA�����EAC��_____�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
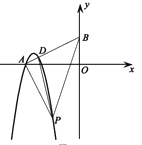
����Ŀ����֪������C��y��(x��2)[t(x��1)��(x��3)]�����У�7��t����2��������t ȡ�κη���������ʵ������A��P ����������C ��.
��1����t����5ʱ����������C �ĶԳ��
��2������60��n����30 ʱ���жϵ㣨1��n���Ƿ���������C�ϣ� ��˵�����ɣ�
��3����ͼ������A��x���ϣ�����A���߶�AP�Ĵ��߽�y���ڵ�B����������C�ڵ�D������D��������Ϊm��![]() ʱ����S��PAD����Сֵ.
ʱ����S��PAD����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������C1��y��ax2+bx��1������A(��2��1)�͵�B(��1����1)��������C2��y��2x2+x+1����ֱ��x��t��������C1���ڵ�N����������C2���ڵ�M��
��1����������C1�ı���ʽ��
��2��ֱ���ú�t�Ĵ���ʽ�����߶�MN�ij���
��3������AMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
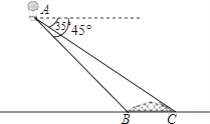
����Ŀ��С����������A�Ͽ�����ǰ�������������Ĵ���BC�������B��C����ĸ��Ƿֱ�Ϊ45�㡢35������֪����BC�������ͬһˮƽ���ϣ��䳤��Ϊ100m���������������ĸ߶ȣ�������������������ο����ݣ�sin35��=0.57��cos35��=0.82��tan35��=0.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
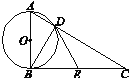
����Ŀ����ͼ����Rt��ABC������ABC��90�㣬��ABΪֱ���ġ�O��AC���ڵ�D��E��BC���е�������BD��DE.
(1)��![]() ����sinC��
����sinC��
(2)��֤��DE�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
����ѧ����ϣ���ʦ�����������⣬��ͬѧ��չ��̽�����
[�����龳]
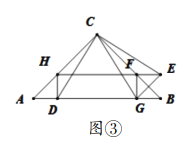
��ͼ�٣���![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() ��һ��
��һ��![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ��Ķ�Ӧ�߶�Ϊ
���õ��Ķ�Ӧ�߶�Ϊ![]() ������
������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����������������������ǡ������ѧ���Ⲣ���
����������������������ǡ������ѧ���Ⲣ���
 ��
�� ����
����
[�������]
������ѧϰС��������������⣬��������Щ���⣺
��1������Ȥ��������������ǣ���֤��![]() ��
��
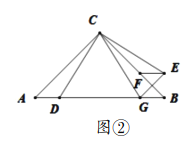
��2����ʵ����С������������ǣ���ͼ�ڣ�����![]() ��
��![]() �Ĵ�ֱƽ���߶��ۣ��õ�
�Ĵ�ֱƽ���߶��ۣ��õ�![]() ������
������![]() �����߶�
�����߶�![]() ��
��![]() ��������������ϵ����˵�����ɣ�
��������������ϵ����˵�����ɣ�
��3�����ܽ���С���ڡ�ʵ����С��̽���Ļ����ϣ�������������⣺�ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ����֤���ı���
����֤���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com