
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
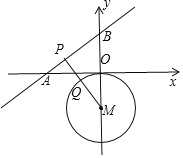
先解方程组![]() 得P点坐标为(3a﹣1,4a+2),则可确定点P为直线y=
得P点坐标为(3a﹣1,4a+2),则可确定点P为直线y=![]() x+
x+![]() 上一动点,设直线y=
上一动点,设直线y=![]() x+
x+![]() 与坐标的交点为A、B,如图,则A(﹣
与坐标的交点为A、B,如图,则A(﹣![]() ,0),B(0,
,0),B(0,![]() ),利用勾股定理计算出AB=
),利用勾股定理计算出AB=![]() ,过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,证Rt△MBP∽Rt△ABO,利用相似比计算出MP=
,过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,证Rt△MBP∽Rt△ABO,利用相似比计算出MP=![]() ,则PQ=
,则PQ=![]() ,即线段PQ的最小值为
,即线段PQ的最小值为![]() .
.
解方程组![]() 得
得![]() ,
,
∴P点坐标为(3a﹣1,4a+2),
设x=3a﹣1,y=4a+2,
∴y=![]() x+
x+![]() ,
,
即点P为直线y=![]() x+
x+![]() 上一动点,
上一动点,
设直线y=![]() x+
x+![]() 与坐标的交点为A、B,如图,则A(﹣
与坐标的交点为A、B,如图,则A(﹣![]() ,0),B(0,
,0),B(0,![]() ),
),
∴AB=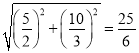
过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小.
∵∠MBP=∠ABO,
∴Rt△MBP∽Rt△ABO,
∴MP:OA=BM:AB,即MP:![]() =
=![]() :
:![]() ,
,
∴MP=![]() ,∴PQ=
,∴PQ=![]() ﹣1=
﹣1=![]() ,
,
即线段PQ的最小值为![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A. 3![]() B. 2
B. 2![]() C. 5 D. 6
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
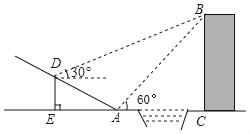
【题目】如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
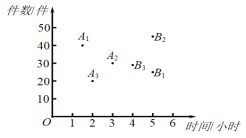
【题目】三名快递员某天的工作情况如图所示,其中点![]() ,
,![]() ,
,![]() 的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点
的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点![]() ,
,![]() ,
,![]() ,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
A. ①②B. ①③C. ②D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P(x1,y1)Q(x2,y2),定义P、Q两点的横坐标之差的绝对值与纵坐标之差的绝对值的和为P、Q两点的直角距离,记作d(P,Q).即d(P,Q)=|x2﹣x1|+|y2﹣y1|
如图1,在平面直角坐标系xOy中,A(1,4),B(5,2),则d(A,B)=|5﹣1|+|2﹣4|=6.
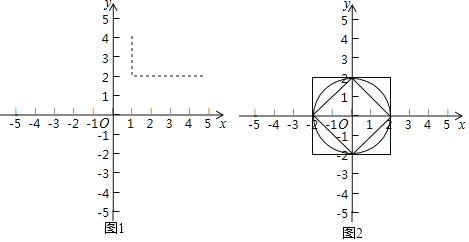
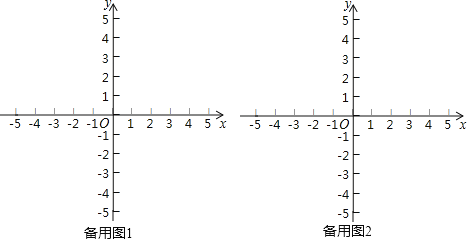
(1)如图2,已知以下三个图形:
①以原点为圆心,2为半径的圆;
②以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形;
③以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形.
点P是上面某个图形上的一个动点,且满足d(O,P)=2总成立.写出符合题意的图形对应的序号 .
(2)若直线y=k(x+3)上存在点P使得d(O,P)=2,求k的取值范围.
(3)在平面直角坐标系xOy中,P为动点,且d(O,P)=3,⊙M圆心为M(t,0),半径为1.若⊙M上存在点N使得PN=1,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
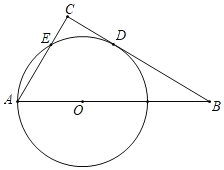
【题目】如图,已知Rt△ABC中,CAB=60°,点O为斜边AB上一点,且OA=2,以OA为半径的⊙O与BC相切于D,与AC交于点E,连接AD.
(1)求线段CD的长;
(2)求⊙O与Rt△ABC重叠部分的面积.(结果保留准确值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字40个,比赛结束后随机抽查部分学生听写“正确的字数”,以下是根据抽查结果绘制的统计图表.
频数分布表
组别 | 正确的字数 | 人数 |
| 0.5~8.5 | 10 |
| 8.5~16.5 | 15 |
| 16.5~24.5 | 25 |
| 24.5~32.5 |
|
| 32.5~40.5 |
|
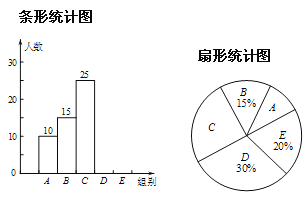
根据以上信息解决下列问题:
(1)补全条形统计图;
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是_________;
组”所对应的圆心角的度数是_________;
(3)若该校共有1210名学生,如果听写正确的字数少于25,则定为不合格;请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在纸上画折线,他每次都是按水平方向画,再按竖直方向画,且每次画完后的两条线段的长度相等,如果第![]() 次画的两条线段的长度都是
次画的两条线段的长度都是![]() ,第
,第![]() 次画的两条线段的长度都为
次画的两条线段的长度都为![]() ,...,第
,...,第![]() 次画的两条线段长度都是
次画的两条线段长度都是![]() ,请你回答下列问题,说明理由.
,请你回答下列问题,说明理由.
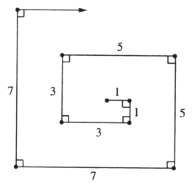
(1)画完第![]() 次后,小明所画的折线的总长度是多少?
次后,小明所画的折线的总长度是多少?
(2)画完第![]() 次后,小明所画的折线的总长度是多少(用含
次后,小明所画的折线的总长度是多少(用含![]() 的代数式表示)?
的代数式表示)?
(3)当小明所画的折线总长度为![]() 时,试求折线的最后两条线段的长度和.
时,试求折线的最后两条线段的长度和.
查看答案和解析>>
科目:初中数学 来源: 题型:
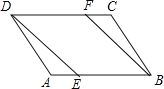
【题目】在平行四边形ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,试判定四边形DEBF是何种特殊四边形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com