
【题目】在平面直角坐标系xOy中,已知P(x1,y1)Q(x2,y2),定义P、Q两点的横坐标之差的绝对值与纵坐标之差的绝对值的和为P、Q两点的直角距离,记作d(P,Q).即d(P,Q)=|x2﹣x1|+|y2﹣y1|
如图1,在平面直角坐标系xOy中,A(1,4),B(5,2),则d(A,B)=|5﹣1|+|2﹣4|=6.
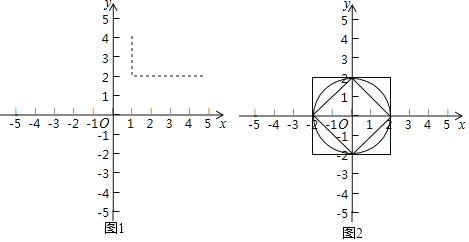
(1)如图2,已知以下三个图形:
①以原点为圆心,2为半径的圆;
②以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形;
③以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形.
点P是上面某个图形上的一个动点,且满足d(O,P)=2总成立.写出符合题意的图形对应的序号 .
(2)若直线y=k(x+3)上存在点P使得d(O,P)=2,求k的取值范围.
(3)在平面直角坐标系xOy中,P为动点,且d(O,P)=3,⊙M圆心为M(t,0),半径为1.若⊙M上存在点N使得PN=1,求t的取值范围.
【答案】(1) ③;(2)﹣![]() ≤k≤
≤k≤![]() ;(3)﹣5≤t≤﹣3+2
;(3)﹣5≤t≤﹣3+2![]() 或3﹣2
或3﹣2![]() ≤t≤5.
≤t≤5.
【解析】
(1)分三种情况设出点P的坐标,按照两点的直角距离的定义可以直接求出结果,即可判断各结论是否符合题意;
(2)分别求出直线y=k(x+3)经过特殊点(0,2),(0,﹣2)时k的值,由运动过程写出k的取值范围;
(3)由(1)可判断满足d(O,P)=3的点是在以原点为中心,对角线在坐标轴上,且对角线长为6的正方形ABCD上,再分别求出⊙M与正方形在y轴左右两边最远距离为2时t的值,即可写出结果.
解:(1)①如图1,点P在以原点为圆心,2为半径的圆上,
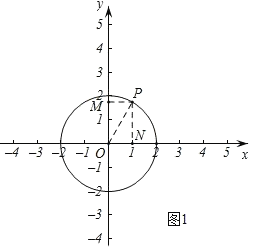
设P点横坐标为1,则纵坐标为![]() ,
,
∴P(1,![]() ),
),
根据定义两点的直角距离,d(P,O)=|2﹣0|+|![]() ﹣0|=2+
﹣0|=2+![]() ≠2,
≠2,
故①不符合题意;
②如图2,点P在以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形上时,
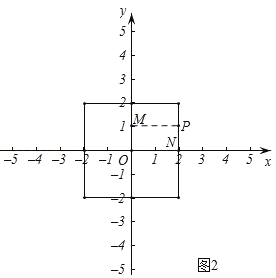
设P(2,a)(a≠0),
则d(P,O)=|2﹣0|+|a﹣0|=2+a≠2,
故②不符合题意;
③如图3,点P在以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形上时,
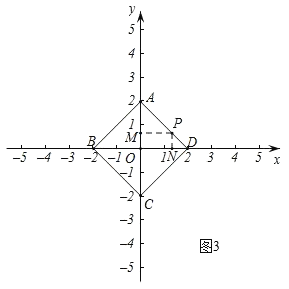
将点A(0,2),D(2,0)代入y=kx+b,
得,![]() ,
,
解得,k=﹣1,b=2,
∴yAD=﹣x+2,
设点P在AD上,坐标为(a,﹣a+2)(0≤a≤2),
则d(P,O)=|a﹣0|+|﹣a+2﹣0|=2,
故③符合题意;
故答案为③;
(2)当直线经过(0,2)时,将(0,2)代入直线y=k(x+3),
得,3k=2,
∴k=![]() ;
;
当直线经过(0,﹣2)时,将(0,﹣2)代入直线y=k(x+3),
得,3k=﹣2,
∴k=﹣![]() ;
;
运动观察可知,k的取值范围为﹣![]() ≤k≤
≤k≤![]() ;
;
(3)由题意,满足d(O,P)=3的点是在以原点为中心,对角线在坐标轴上,且对角线长为6的正方形ABCD上(如图4),
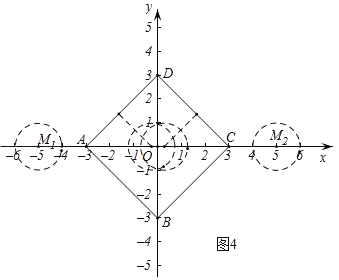
当M在正方形ABCD外时,若MA=2,则t=﹣5,若MC=2,则t=5,
当M在正方形ABCD内部时,
若M到正方形AD,AB边的距离恰好为2,
则t=﹣3+2![]() ,
,
若M到正方形DC,BC边的距离恰好为2,
则t=3﹣2![]() ,
,
运动观察可知,t的取值范围为﹣5≤t≤﹣3+2![]() 或3﹣2
或3﹣2![]() ≤t≤5.
≤t≤5.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
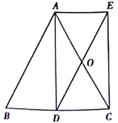
【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
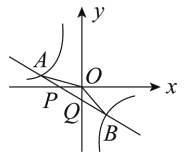
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() .给出下列结论:
.给出下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④不等式
;④不等式![]() 的解集是
的解集是![]() 或
或![]() .
.
其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级举行了“中国梦”演讲比赛活动,学校团委根据学生的成绩划分为A,B,C,D四个等级,并绘制了如下两个不完整的两种统计图.
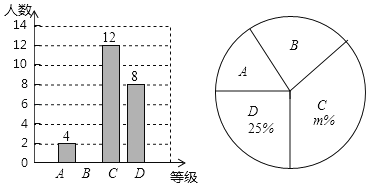
根据图中提供的信息,回答下列问题
(1)参加演讲比赛的学生共有 人,并把条形图补充完整;
(2)扇形统计图中,m= ;C等级对应的扇形的圆心角为 度.
(3)学校准备从获得A等级的学生中随机选取2人,参加全市举办的演讲比赛,请利用列表法或树状图法,求获得A等级的小明参加市比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后2分钟内,两人相遇的次数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
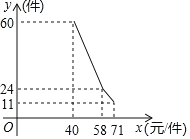
【题目】某店因为经营不善欠下38000元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息)已知该店代理的某品牌服装的进价为每件40元,该品牌服装日的售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)当销售价为多少元时,该店的日销售利润最大;
(3)该店每天支付工资和其它费用共250元,该店能否在一年内还清所有债务.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为![]() 的直径,
的直径,![]() 为圆弧上的一点,
为圆弧上的一点,![]() ,垂足为D,AC平分
,垂足为D,AC平分![]() ,AB的延长线交直线
,AB的延长线交直线![]() 于点
于点![]() .
.
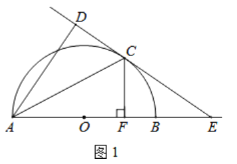
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,B为
,B为![]() 的中点,
的中点,![]() ,垂足为点
,垂足为点![]() ,求
,求![]() 的长;
的长;
(3)如图2,连接OD交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
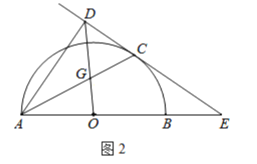
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
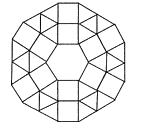
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com