
【题目】如图已知直线![]() 直线
直线![]() 和直线
和直线![]() 交于点C和D,在C、D之间有一点P.
交于点C和D,在C、D之间有一点P.
(1)图中∠PAC、∠APB、∠PBD之间有什么关系,并说明理由;
(2)如果P点在C、D之间运动时,∠PAC、∠APB、∠PBD之间的关系是否发生变化?
(3)若点P在直线![]() 上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。

【答案】(1)∠APB=∠CAP+∠DBP;(2)不发生变化;(3)当P点在DC延长线上时:∠APB=∠DBP-∠CAP;当P点在CD延长线上时:∠APB=∠CAP-∠DBP
【解析】
(1)过点P作EP∥a,根据平行线的性质即可求解;
(2)根据平行线的性质可知不会发生变化;
(3)根据题意作出图形,根据平行线的性质即可求解.
(1)如图,过点P作EP∥a,
∵![]()
∴EP∥a∥b,
∴∠CAP=∠1,∠DBP=∠2,
∵∠APB=∠1+∠2,
∴∠APB=∠CAP+∠DBP
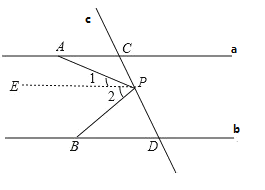
(2)当P点在C、D之间运动时,∠APB=∠CAP+∠DBP,不会发生变化;
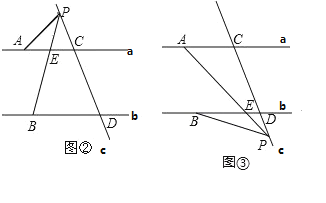
(3)如图②,当P点在DC延长线上时:∠APB=∠DBP-∠CAP.
理由如下:
∵a∥b,∴∠PEC=∠PBD,
∵∠PEC=∠CAP +∠APB
∴∠PBD=∠CAP +∠APB
即∠APB=∠DBP-∠CAP.
如图③当P点在CD延长线上时:∠APB=∠CAP-∠DBP
理由如下:
∵a∥b,∴∠CAP =∠DEP,
∵∠DEP =∠DBP +∠APB
∴∠CAP =∠DBP +∠APB
即∠APB=∠CAP-∠DBP


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
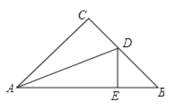
A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,对角线AC、BD交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°.
(1)求证:△AOB是等边三角形;
(2)求∠BOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠3=∠E.则AD与BE平行吗?
完成下面的解答过程(填写理由或数学式).
解:∵∠1=∠2(已知),
∴ ∥ (内错角相等,两直线平行),
∴∠E=∠ (两直线平行,内错角相等),
又∵∠E=∠3(已知),
∴∠3=∠ (等量代换),
∴AD∥BE( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图像经过点
的图像经过点![]() .
.
(![]() )求该二次函数的关系式.
)求该二次函数的关系式.
(![]() )证明:无论
)证明:无论![]() 取何值,函数值
取何值,函数值![]() 总不等于
总不等于![]() .
.
(![]() )将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
)将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,∠MON =70°,点A、B在∠MON的两条边上运动,∠MAB与∠NBA的平分线交于点P.
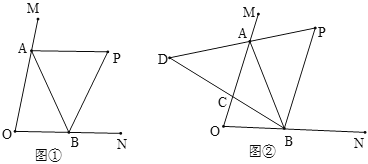
(1)点A、B在运动过程中,∠P的大小会变吗?若不会,求∠P的度数;若会,请说明理由.
(2)如图②,继续作BC平分∠ABO,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?若不会,求出∠D的度数;若会,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com