
【题目】二次函数![]() 的图像经过点
的图像经过点![]() .
.
(![]() )求该二次函数的关系式.
)求该二次函数的关系式.
(![]() )证明:无论
)证明:无论![]() 取何值,函数值
取何值,函数值![]() 总不等于
总不等于![]() .
.
(![]() )将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
)将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
【答案】(1)![]() ;(2)答案见解析;(3)左,1,下,2.
;(2)答案见解析;(3)左,1,下,2.
【解析】试题分析:(1)直接将(3,6)点代入即可求出a的值;
(2)直接利用配方法求出二次函数最值进而得出判断即可;
(3)直接利用二次函数平移规律得出答案.
试题解析:(1)解:将(3,6)代入y=ax2﹣2x+3得:
6=9a﹣6+3,解得:a=1,故抛物线解析式为:y=x2﹣2x+3;
(2)证明:∵y=x2﹣2x+3=(x﹣1)2+2,∴函数值y有最小值2,故无论x取何值,函数值y总不等于1;
(3)解:将该抛物线先向左平移1单位,得到y=x2+2,再向下平移2个单位,得到y=x2,该抛物线的顶点为原点.
故答案为:左,1,下,2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作出函数y=﹣x+3的图象,并利用图象回答问题:
(1)当y<0时,x的取值范围为_____;
(2)当﹣2<x<2时,y的取值范围为_____;
(3)图象与直线y=x﹣1的交点坐标为______;这两条直线与y轴围成的三角形面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知直线![]() 直线
直线![]() 和直线
和直线![]() 交于点C和D,在C、D之间有一点P.
交于点C和D,在C、D之间有一点P.
(1)图中∠PAC、∠APB、∠PBD之间有什么关系,并说明理由;
(2)如果P点在C、D之间运动时,∠PAC、∠APB、∠PBD之间的关系是否发生变化?
(3)若点P在直线![]() 上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
查看答案和解析>>
科目:初中数学 来源: 题型:
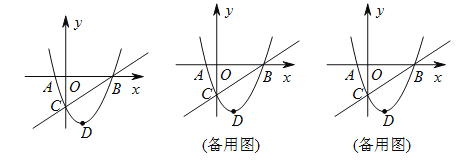
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线顶点,点
是抛物线顶点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(![]() )这个二次函数的表达式为____________.
)这个二次函数的表达式为____________.
(![]() )设直线
)设直线![]() 的解析式为
的解析式为![]() ,则不等式
,则不等式![]() 的解集为___________.
的解集为___________.
(![]() )连结
)连结![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(![]() )当四边形
)当四边形![]() 的面积最大时,求出此时
的面积最大时,求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
(![]() )若把条件“点
)若把条件“点![]() 是直线
是直线![]() 下方的抛物线上一动点.”改为“点
下方的抛物线上一动点.”改为“点![]() 是抛物线上的任一动点”,其它条件不变,当以
是抛物线上的任一动点”,其它条件不变,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为梯形时,直接写出点
为顶点的四边形为梯形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有__次.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com