
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¶ž“ĪŗÆŹż![]() µÄĶ¼ĻńÓė
µÄĶ¼ĻńÓė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() ”¢
”¢![]() Į½µć£¬Óė
Į½µć£¬Óė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() µć£¬µć
µć£¬µć![]() ŹĒÅ×ĪļĻ߶„µć£¬µć
ŹĒÅ×ĪļĻ߶„µć£¬µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ĻĀ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£®
ĻĀ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£®
£Ø![]() £©Õāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½ĪŖ____________£®
£©Õāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½ĪŖ____________£®
£Ø![]() £©ÉčÖ±Ļß
£©ÉčÖ±Ļß![]() µÄ½āĪöŹ½ĪŖ
µÄ½āĪöŹ½ĪŖ![]() £¬Ōņ²»µČŹ½
£¬Ōņ²»µČŹ½![]() µÄ½ā¼ÆĪŖ___________£®
µÄ½ā¼ÆĪŖ___________£®
£Ø![]() £©Į¬½į
£©Į¬½į![]() ”¢
”¢![]() £¬²¢°Ń
£¬²¢°Ń![]() ŃŲ
ŃŲ![]() ·ÕŪ£¬µĆµ½ĖıߊĪ
·ÕŪ£¬µĆµ½ĖıߊĪ![]() £¬ÄĒĆ“ŹĒ·ń“ęŌŚµć
£¬ÄĒĆ“ŹĒ·ń“ęŌŚµć![]() £¬Ź¹ĖıߊĪ
£¬Ź¹ĖıߊĪ![]() ĪŖĮāŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±µć
ĪŖĮāŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±µć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø![]() £©µ±ĖıߊĪ
£©µ±ĖıߊĪ![]() µÄĆ껿×ī“óŹ±£¬Ēó³ö“ĖŹ±
µÄĆ껿×ī“óŹ±£¬Ēó³ö“ĖŹ±![]() µćµÄ×ų±źŗĶĖıߊĪ
µćµÄ×ų±źŗĶĖıߊĪ![]() µÄ×ī“óĆ껿£®
µÄ×ī“óĆ껿£®
£Ø![]() £©Čō°ŃĢõ¼ž”°µć
£©Čō°ŃĢõ¼ž”°µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ĻĀ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£®”±øÄĪŖ”°µć
ĻĀ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£®”±øÄĪŖ”°µć![]() ŹĒÅ×ĪļĻßÉĻµÄČĪŅ»¶Æµć”±£¬ĘäĖüĢõ¼ž²»±ä£¬µ±ŅŌ
ŹĒÅ×ĪļĻßÉĻµÄČĪŅ»¶Æµć”±£¬ĘäĖüĢõ¼ž²»±ä£¬µ±ŅŌ![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ĪŖ¶„µćµÄĖıߊĪĪŖĢŻŠĪŹ±£¬Ö±½ÓŠ“³öµć
ĪŖ¶„µćµÄĖıߊĪĪŖĢŻŠĪŹ±£¬Ö±½ÓŠ“³öµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©x”Ü0»ņx”Ż3£»£Ø3£©
£»£Ø2£©x”Ü0»ņx”Ż3£»£Ø3£©![]() £»£Ø4£©µ±P£Ø
£»£Ø4£©µ±P£Ø![]() £¬
£¬![]() £©Ź±£¬SĖıߊĪABPC×ī“ó
£©Ź±£¬SĖıߊĪABPC×ī“ó![]() £»£Ø5£©µćPµÄ×ų±źĪŖ£Ø£2£¬5£©£¬£Ø2£¬£3£©»ņ£Ø4£¬5£©£®
£»£Ø5£©µćPµÄ×ų±źĪŖ£Ø£2£¬5£©£¬£Ø2£¬£3£©»ņ£Ø4£¬5£©£®
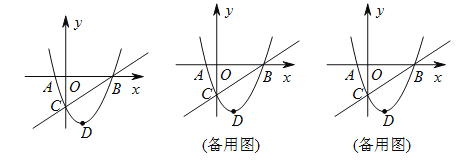
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Ö±½ÓÉč³É¶„µćŹ½¼“æÉµĆ³öÅ×ĪļĻß½āĪöŹ½£»
£Ø2£©ĻČČ·¶Ø³öµćB£¬C×ų±ź£¬ŌŁøł¾ŻĶ¼ĻóÖ±½ÓŠ“³ö·¶Ī§£»
£Ø3£©ĄūÓĆĮāŠĪµÄŠŌÖŹµĆ³öPO=PC¼“æÉµĆ³öµćPµÄׯ×ų±ź£¬“śČėÅ×ĪļĻß½āĪöŹ½¼“æÉµĆ³ö½įĀŪ£»
£Ø4£©ĻČĄūÓĆ×ų±źĻµÖŠ¼øŗĪĶ¼ŠĪµÄĆ껿µÄ¼ĘĖć·½·Ø½ØĮ¢ŗÆŹż¹ŲĻµŹ½¼“æÉĒó³öĆ껿µÄ×ī“óÖµ£»
£Ø5£©ĻČĒó³öÖ±ĻßBC£¬BC£¬CDµÄ½āĪöŹ½£¬·ÖČżÖÖĒéæöĄūÓĆĢŻŠĪµÄŠŌÖŹ£¬Ņ»×é¶Ō±ßĘ½ŠŠ¼“æÉµĆ³öÖ±ĻßDP1£¬CP2£¬BP3µÄ½āĪöŹ½£¬·Ö±šĮŖĮ¢Å×ĪļĻߵĽāĪöŹ½½ØĮ¢·½³Ģ×éĒó½ā¼“æÉ£®
ŹŌĢā½āĪö£ŗ½ā£ŗ£Ø1£©”ßµćD£Ø1£¬©4£©ŹĒÅ×ĪļĻßy=x2+bx+cµÄ¶„µć£¬”ąy=£Øx©1£©2©4=x2©2x©3£®¹Ź“š°øĪŖ£ŗy=x2©2x©3£»
£Ø2£©Įīx=0£¬”ąy=©3£¬”ąC£Ø0£¬©3£©£¬Įīy=0£¬”ąx2©2x©3=0£¬”ąx=©1»ņx=3£¬”ąA£Ø©1£¬0£©£¬B£Ø3£¬0£©£¬”ą²»µČŹ½x2+bx+c”Żkx+mµÄ½ā¼ÆĪŖx£¼0»ņ£¾3£®¹Ź“š°øĪŖ£ŗx£¼0»ņ£¾3£»
£Ø3£©ČēĶ¼1£®”ßĖıߊĪPOP”äCĪŖĮāŠĪ£¬”ąPO=PC£®”ßC£Ø0£¬©3£©£¬”ąµćPµÄׯ×ų±źĪŖ©![]() £®”ßPŌŚÅ×ĪļĻßy=x2©2x©3ÉĻ£¬”ą©
£®”ßPŌŚÅ×ĪļĻßy=x2©2x©3ÉĻ£¬”ą©![]() =x2©2x©3£¬”ąx=
=x2©2x©3£¬”ąx=![]() »ņx=
»ņx=![]() £ØÉį£©£¬”ąP£Ø
£ØÉį£©£¬”ąP£Ø![]() £®©
£®©![]() £©£»
£©£»
£Ø4£©ČēĶ¼2£¬ÓÉ£Ø1£©ÖŖ£¬B£Ø3£¬0£©£¬C£Ø0£¬©3£©£¬”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=x©3£¬¹żµćP×÷PE”ĪyÖį½»BCÓŚE£¬ÉčP£Øm£¬m2©2m©3£©£¬£Ø0£¼m£¼3£©
”ąE£Øm£¬m©3£©£¬”ąPE=m©3©£Øm2©2m©3£©=©m2+3m£®”ßA£Ø©1£¬0£©£¬B£Ø3£¬0£©£¬C£Ø0£¬©3£©£¬”ąSĖıߊĪABPC=S”÷ABC+S”÷PCE+S”÷PBE=![]() ABOC+
ABOC+![]() PE|xP|+
PE|xP|+![]() PE|xB©xP|
PE|xB©xP|
=![]() ABOC+
ABOC+![]() PE£Ø|xP|+|xB©xP|£©=
PE£Ø|xP|+|xB©xP|£©=![]() ”Į4”Į3+
”Į4”Į3+![]() £Ø©m2+3m£©”Į£Øm+3©m£©
£Ø©m2+3m£©”Į£Øm+3©m£©
=6+![]() ”Į£Ø©m2+3m£©=©
”Į£Ø©m2+3m£©=©![]() £Øm©
£Øm©![]() £©2+
£©2+![]()
µ±m=![]() Ź±£¬SĖıߊĪABPC×ī“ó=
Ź±£¬SĖıߊĪABPC×ī“ó=![]() £®
£®
µ±m=![]() Ź±£¬m2©2m©3=
Ź±£¬m2©2m©3=![]() £¬”ąP£Ø
£¬”ąP£Ø![]() £¬
£¬![]() £©£®
£©£®
£Ø5£©ČēĶ¼£¬ÓÉ£Ø1£©ÖŖ£¬B£Ø3£¬0£©£¬C£Ø0£¬©3£©£¬D£Ø1£¬©4£©£¬”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=x©3£¬Ö±ĻßBDµÄ½āĪöŹ½ĪŖy=2x©6£¬Ö±ĻßCDµÄ½āĪöŹ½ĪŖy=©x©3£®”ßŅŌP”¢C”¢D”¢BĪŖ¶„µćµÄĖıߊĪĪŖĢŻŠĪ£®”ßÅ×ĪļĻߵĽāĪöŹ½ĪŖy=x2©2x©3¢Ł£»
¢Łµ±DP1”ĪBCŹ±£¬”ąÖ±ĻßDP1µÄ½āĪöŹ½ĪŖy=x©5¢Ś£¬ĮŖĮ¢¢Ł¢Ś½āµĆ£¬µćP1£Ø2£¬©3£©£¬[ĮķŅ»øöµćĪŖ£Ø1£¬©4£©ŗĶµćDÖŲŗĻ£¬ÉįČ„]
¢Śµ±CP2”ĪBDŹ±£¬”ąÖ±ĻßCP2µÄ½āĪöŹ½ĪŖy=2x©3¢Ū£¬ĮŖĮ¢¢Ł¢Ū½āµĆµćP2£Ø4£¬5£©
¢Ūµ±BP3”ĪCDŹ±£¬”ąÖ±ĻßBP3”ĪCDµÄ½āĪöŹ½ĪŖy=©x+3¢Ü£¬ĮŖĮ¢¢Ł¢Ü½āµĆµćP3£Ø©2£¬5£©£®
×ŪÉĻĖłŹö£ŗŅŌP”¢C”¢D”¢BĪŖ¶„µćµÄĖıߊĪĪŖĢŻŠĪŹ±£¬µćPµÄ×ų±źĪŖ£Ø©2£¬5£©”¢£Ø2£¬©3£©»ņ£Ø4£¬5£©£®




| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĪŖĮĖøüŗƵŲæŖÕ¹”°Ńō¹āĢåÓżŅ»Š”Ź±”±»ī¶Æ£¬¶Ō±¾Š£Ń§Éś½ųŠŠĮĖ”°Š“³öÄć×īĻ²»¶µÄĢåÓż»ī¶ÆĻīÄæ£ØÖ»Š“Ņ»Ļī£©”±µÄĖ껜³éŃłµ÷²é£¬ĻĀĆęŹĒøł¾ŻµĆµ½µÄĻą¹ŲŹż¾Ż»ęÖʵÄĶ³¼ĘĶ¼µÄŅ»²æ·Ö.
³éŃłµ÷²éѧɜ×īĻ²»¶µÄŌĖ¶ÆĻīÄæµÄČĖŹżĶ³¼ĘĶ¼ ø÷ŌĖ¶ÆĻīÄæµÄĻ²»¶ČĖŹżÕ¼³éŃł×ÜČĖŹż°Ł·Ö±ČĶ³¼ĘĶ¼

Ēėøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©øĆŠ£¶Ō________Ćūѧɜ½ųŠŠĮĖ³éŃłµ÷²é£»
£Ø2£©Ēė½«Ķ¼1ŗĶĶ¼2²¹³äĶźÕū£»
£Ø3£©Ķ¼2ÖŠĢųÉžĖłŌŚµÄÉČŠĪ¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹżŹĒ________£»
£Ø4£©ČōøĆŠ£¹²ÓŠ2400ĆūĶ¬Ń§£¬ĒėĄūÓĆŃł±¾Źż¾Ż¹Ą¼ĘČ«Š£Ń§ÉśÖŠ×īĻ²»¶ĢųÉžŌĖ¶ÆµÄČĖŹżŌ¼ĪŖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻC=90”ć£¬AC=BC£¬ADĘ½·Ö”ĻCAB½»BCÓŚµćD£¬DE”ĶAB£¬“¹×ćĪŖE£¬ĒŅAB=6cm£¬Ōņ”÷DEBµÄÖܳ¤ĪŖ£Ø £©
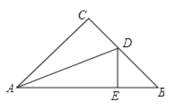
A. 4cm B. 6cm C. 8cm D. 10cm
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”Ļ1£½”Ļ2£¬”Ļ3£½”ĻE£®ŌņADÓėBEĘ½ŠŠĀš£æ
Ķź³ÉĻĀĆęµÄ½ā“š¹ż³Ģ£ØĢīŠ“ĄķÓÉ»ņŹżŃ§Ź½£©£®
½ā£ŗ”ß”Ļ1£½”Ļ2£ØŅŃÖŖ£©£¬
”ą ”Ī £ØÄŚ“ķ½ĒĻąµČ£¬Į½Ö±ĻßĘ½ŠŠ£©£¬
”ą”ĻE£½”Ļ £ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©£¬
Ó֔ߔĻE£½”Ļ3£ØŅŃÖŖ£©£¬
”ą”Ļ3£½”Ļ £ØµČĮæ“ś»»£©£¬
”ąAD”ĪBE£Ø £©£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹż![]() µÄĶ¼Ļń¾¹żµć
µÄĶ¼Ļń¾¹żµć![]() £®
£®
£Ø![]() £©Ēóøƶž“ĪŗÆŹżµÄ¹ŲĻµŹ½£®
£©Ēóøƶž“ĪŗÆŹżµÄ¹ŲĻµŹ½£®
£Ø![]() £©Ö¤Ć÷£ŗĪŽĀŪ
£©Ö¤Ć÷£ŗĪŽĀŪ![]() Č”ŗĪÖµ£¬ŗÆŹżÖµ
Č”ŗĪÖµ£¬ŗÆŹżÖµ![]() ×ܲ»µČÓŚ
×ܲ»µČÓŚ![]() £®
£®
£Ø![]() £©½«øĆÅ×ĪļĻßĻČĻņ___________£ØĢī”°×ó”±»ņ”°ÓŅ”±£©Ę½ŅĘ___________øöµ„Ī»£¬ŌŁĻņ___________£ØĢī”°ÉĻ”±»ņ”°ĻĀ”±£©Ę½ŅĘ___________øöµ„Ī»£¬Ź¹µĆøĆÅ×ĪļĻߵĶ„µćĪŖŌµć£®
£©½«øĆÅ×ĪļĻßĻČĻņ___________£ØĢī”°×ó”±»ņ”°ÓŅ”±£©Ę½ŅĘ___________øöµ„Ī»£¬ŌŁĻņ___________£ØĢī”°ÉĻ”±»ņ”°ĻĀ”±£©Ę½ŅĘ___________øöµ„Ī»£¬Ź¹µĆøĆÅ×ĪļĻߵĶ„µćĪŖŌµć£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
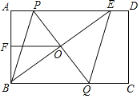
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬EŹĒADÉĻŅ»µć£¬PQ“¹Ö±Ę½·ÖBE£¬·Ö±š½»AD£¬BE£¬BCÓŚµćP£¬O£¬Q£¬Į¬½ÓBP£¬EQ£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪBPEQŹĒĮāŠĪ£»
£Ø2£©FĪŖABµÄÖŠµć£¬ŌņĻ߶ĪOFÓėĻ߶ĪAEÓŠŹ²Ć“Ī»ÖĆ¹ŲĻµŗĶŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ČōAB£½6£¬OF£½4£¬ĒóPQµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬”ĻMON =70”ć£¬µćA”¢BŌŚ”ĻMONµÄĮ½Ģõ±ßÉĻŌĖ¶Æ£¬”ĻMABÓė”ĻNBAµÄĘ½·ÖĻß½»ÓŚµćP£®
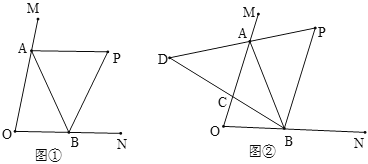
£Ø1£©µćA”¢BŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬”ĻPµÄ“óŠ”»į±äĀš£æČō²»»į£¬Ēó”ĻPµÄ¶ČŹż£»Čō»į£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø2£©ČēĶ¼¢Ś£¬¼ĢŠų×÷BCĘ½·Ö”ĻABO£¬APµÄ·“ĻņŃÓ³¤Ļß½»BCµÄŃÓ³¤ĻßÓŚµćD£¬µćA”¢BŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬”ĻDµÄ“óŠ”»į±äĀš£æČō²»»į£¬Ēó³ö”ĻDµÄ¶ČŹż£»Čō»į£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪÖ½Ę¬ABCDÖŠ£¬AB=3£¬BC=9£®½«¾ŲŠĪÖ½Ę¬ÕŪµž£¬Ź¹µćBŗĶµćDÖŲŗĻ£®
£Ø1£©ĒóEDµÄ³¤£»
£Ø2£©ĒóÕŪŗŪEFµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĒė“ÓŅŌĻĀĖÄøöŅ»ŌŖ¶ž“Ī·½³ĢÖŠČĪєȿøö£¬²¢ÓĆŹŹµ±µÄ·½·Ø½āÕāČżøö·½³Ģ£®
£Ø1£©x2©x©1=0£»
£Ø2£©£Øy©2£©2©12=0£»
£Ø3£©£Ø1+m£©2=m+1£»
£Ø4£©t2©4t=5£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com