
【题目】如图,在矩形纸片ABCD中,AB=3,BC=9.将矩形纸片折叠,使点B和点D重合.
(1)求ED的长;
(2)求折痕EF的长.

【答案】(1)5;(2)![]()
【解析】
(1)先依据翻折的性质和平行线的性质证明三角形DEF为等腰三角形,从而得到ED=DF,设DE=x,则DF=x,FC=9-x,然后在△DFC中依据勾股定理列方程求解即可;
(2)过点E做EM垂直于BC,垂足为M.先求得MF的长度,然后依据勾股定理可求得EF的长.
解:(1)∵四边形ABCD为矩形,
∴AB=CD=3.
∵AD∥BC,
∴∠BFE=∠DEF.
∵∠BFE=∠EFD,
∴∠EFD=∠DEF,
∴DE=DF.
设DE=x,则DF=x,FC=9﹣x.
在Rt△DFC中,FC2+DC2=DF2,
∴(9﹣x)2+32=x2.解得x=5.
∴DE=5.
(2)过点E做EM垂直于BC,垂足为M.
根据(1)可知BF=DF=5,![]()
![]()
![]() AE=CF=4,
AE=CF=4,

∵AE=CF=4,BF=DF=5,
∴MF=BF﹣BM=5﹣4=1.
∴Rt△MEF中,EF2=EM2+MF2=32+12=10
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
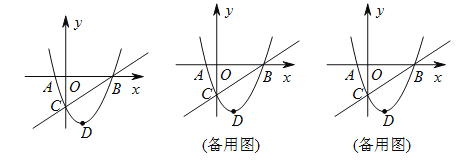
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线顶点,点
是抛物线顶点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(![]() )这个二次函数的表达式为____________.
)这个二次函数的表达式为____________.
(![]() )设直线
)设直线![]() 的解析式为
的解析式为![]() ,则不等式
,则不等式![]() 的解集为___________.
的解集为___________.
(![]() )连结
)连结![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(![]() )当四边形
)当四边形![]() 的面积最大时,求出此时
的面积最大时,求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
(![]() )若把条件“点
)若把条件“点![]() 是直线
是直线![]() 下方的抛物线上一动点.”改为“点
下方的抛物线上一动点.”改为“点![]() 是抛物线上的任一动点”,其它条件不变,当以
是抛物线上的任一动点”,其它条件不变,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为梯形时,直接写出点
为顶点的四边形为梯形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有__次.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() 、
、![]() 两点对应的有理数分別为
两点对应的有理数分別为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 分别同时从点
分别同时从点![]() 和点
和点![]() 出发,以每秒
出发,以每秒![]() 个单位长度,每秒
个单位长度,每秒![]() 个单位长度的速度向数轴正方向运动,设运动时间为
个单位长度的速度向数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)当![]() 时,则
时,则![]() 、
、![]() 两点对应的有理数分别是______;
两点对应的有理数分别是______;![]() _______;
_______;
(2)点![]() 是数轴上点
是数轴上点![]() 左侧一点,其对应的数是
左侧一点,其对应的数是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在点![]() 和点
和点![]() 出发的同时,点
出发的同时,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,开始向左运动,遇到点
出发,开始向左运动,遇到点![]() 后立即返回向右运动,遇到点
后立即返回向右运动,遇到点![]() 后立即返回向左运动,与点
后立即返回向左运动,与点![]() 相遇后再立即返回,如此往返,直到
相遇后再立即返回,如此往返,直到![]() 、
、![]() 两点相遇时,点
两点相遇时,点![]() 停止运动,求点
停止运动,求点![]() 运动的路程一共是多少个单位长度?点
运动的路程一共是多少个单位长度?点![]() 停止的位置所对应的数是多少?
停止的位置所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )

A. 12B. 24C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数。
例如,![]() 展开式中的系数1、2、1恰好对应图中第三行的数字;
展开式中的系数1、2、1恰好对应图中第三行的数字;
再如,![]() 展开式中的系数1、3、3、1恰好对应图中第四行的数字。
展开式中的系数1、3、3、1恰好对应图中第四行的数字。
请认真观察此图,写出(a+b)4的展开式,(a+b)4=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.

(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com