练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在菱形ABCD中，∠B＝∠EAF＝60°，∠BAE＝20°，则∠AEF的大小是_____．

    【答案】60°

    【解析】

    由菱形的性质可证△ABC，△ACD都是等边三角形，可得∠B＝∠ACF＝∠BAC＝60°，则可证△ABE≌△ACF，可得AE＝AF，即可证△AEF是等边三角形，即可求∠AEF的大小．

    解：连接AC

    ∵四边形ABCD是菱形

    ∴AB＝BC＝CD＝AD，∠B＝∠D＝60°

    ∴△ABC，△ACD都是等边三角形

    ∴AC＝AB，∠B＝∠ACD＝60°＝∠BAC

    ∵∠BAC＝60°＝∠EAF

    ∴∠BAE＝∠CAF

    又∵AC＝AB，∠B＝∠ACD＝60°

    ∴△ABE≌△ACF

    ′∴AE＝AF且∠EAF＝60°

    ∴△AEF是等边三角形

    ∴∠AEF＝60°

    故答案为60°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点．将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．

    试猜想线段BE和EC的数量及位置关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了更好地开展“阳光体育一小时”活动，对本校学生进行了“写出你最喜欢的体育活动项目（只写一项）”的随机抽样调查，下面是根据得到的相关数据绘制的统计图的一部分.

    抽样调查学生最喜欢的运动项目的人数统计图 各运动项目的喜欢人数占抽样总人数百分比统计图

    请根据以上信息解答下列问题：

    （1）该校对________名学生进行了抽样调查；

    （2）请将图1和图2补充完整；

    （3）图2中跳绳所在的扇形对应的圆心角的度数是________；

    （4）若该校共有2400名同学，请利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平面直角坐标系内两点A、B，点，点B与点A关于y轴对称.

    （1）则点B的坐标为________；

    （2）动点P、Q分别从A点、B点同时出发，沿直线AB向右运动，同向而行，点P的速度是每秒4个单位长度，点Q的速度是每秒2个单位长度，设P、Q的运动时间为t秒，用含t的代数式表示的面积S，并写出t的取值范围；

    （3）在平面直角坐标系中存在一点，满足.求m的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们定义：如图，在△中，把绕点按顺时针方向旋转得到，把绕点按逆时针方向旋转得到，连接，当时，我们称△是△的“旋补三角形”，△边上的中线叫做的“旋补中线”，点叫做“旋补中心”．

    ⑴ 特例感知：在如图、如图中，是的“旋补三角形”，是的“旋补中线”.

    ① 如图，当为等边三角形时，与的数量关系为＝ ；

    ② 如图，当，时，则长为 .

    ⑵ 精确作图：如图，已知在四边形内部存在点，使得是的“旋补三角形”（点D的对应点为点A，点C的对应点为点B），请用直尺和圆规作出点（要求：保留作图痕迹，不写作法和证明）

    ⑶ 猜想论证：在如图中，当△为任意三角形时，猜想与的数量关系，并给予证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知AB∥CD，EF交AB于E，交CD于F，∠AEF＝68°，FG平分∠EFD，KF⊥FG，求∠KFC的度数.

    解：∵AB∥CD(已知)

    ∴∠EFD＝∠AEF( )

    ∵∠AEF＝68°(已知)

    ∴∠EFD＝∠AEF＝68°( )

    ∵FG平分∠EFD(已知)

    所以∠EFG＝∠GFD＝∠EFD＝34°( )

    又因为KF⊥FG( )

    所以∠KFG＝90°( )

    所以∠KFC＝180°－∠GFD－∠KFG＝ .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且AB=6cm，则△DEB的周长为（ ）

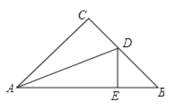
    A. 4cm B. 6cm C. 8cm D. 10cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＝∠2，∠3＝∠E．则AD与BE平行吗？

    完成下面的解答过程（填写理由或数学式）．

    解：∵∠1＝∠2（已知），

    ∴ ∥ （内错角相等，两直线平行），

    ∴∠E＝∠ （两直线平行，内错角相等），

    又∵∠E＝∠3（已知），

    ∴∠3＝∠ （等量代换），

    ∴AD∥BE（ ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形纸片ABCD中，AB=3，BC=9．将矩形纸片折叠，使点B和点D重合．

    （1）求ED的长；

    （2）求折痕EF的长．

    查看答案和解析>>

    同步练习册答案