【题目】如图，已知∠1＝∠2，∠3＝∠E．则AD与BE平行吗？
完成下面的解答过程（填写理由或数学式）．
解：∵∠1＝∠2（已知），
∴ ∥ （内错角相等，两直线平行），
∴∠E＝∠ （两直线平行，内错角相等），
又∵∠E＝∠3（已知），
∴∠3＝∠ （等量代换），
∴AD∥BE（ ）．
科目：初中数学 来源： 题型：
【题目】我们定义：如图，在△
中，把
绕点
按顺时针方向旋转
得到
，把
绕点按逆时针方向旋转
得到
，连接
，当
时，我们称△
是△的“旋补三角形”，△边上的中线
叫做
的“旋补中线”，点叫做“旋补中心”．
⑴ 特例感知：在如图、如图中，
是的“旋补三角形”，是的“旋补中线”.
① 如图，当为等边三角形时，与
的数量关系为＝ ；
② 如图，当
，
时，则长为 .
⑵ 精确作图：如图，已知在四边形
内部存在点
，使得
是
的“旋补三角形”（点D的对应点为点A，点C的对应点为点B），请用直尺和圆规作出点（要求：保留作图痕迹，不写作法和证明）
⑶ 猜想论证：在如图中，当△为任意三角形时，猜想与的数量关系，并给予证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图已知直线
直线
和直线
交于点C和D，在C、D之间有一点P.
(1)图中∠PAC、∠APB、∠PBD之间有什么关系，并说明理由；
(2)如果P点在C、D之间运动时，∠PAC、∠APB、∠PBD之间的关系是否发生变化?
(3)若点P在直线上C、D两点的外侧运动时(点P与点C、D不重合)，试探究∠PAC、∠APB、∠PBD之间的关系又是如何？分别画出图形并说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
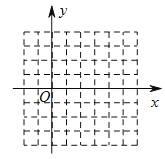
【题目】请在网格坐标系中画出二次函数
的大致图象（注：图中小正方形网格的边长为
），根据图象填空：
（）当
__________时，
有最__________值
__________．
（
）随
的增大而减小的自变量的取值范围是__________．
（
）结合图象直接写出
时的范围：__________．
（
）结合图象直接写出
时的取值范围：__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
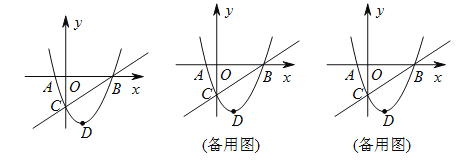
【题目】如图，在平面直角坐标系中，二次函数
的图像与
轴交于
、
两点，与
轴交于
点，点
是抛物线顶点，点
是直线
下方的抛物线上一动点．
（
）这个二次函数的表达式为____________．
（
）设直线的解析式为
，则不等式
的解集为___________．
（
）连结
、
，并把
沿
翻折，得到四边形
，那么是否存在点，使四边形为菱形？若存在，请求出此时点的坐标；若不存在，请说明理由．
（
）当四边形
的面积最大时，求出此时点的坐标和四边形的最大面积．
（
）若把条件“点是直线下方的抛物线上一动点．”改为“点是抛物线上的任一动点”，其它条件不变，当以、、
、为顶点的四边形为梯形时，直接写出点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数。
例如，
展开式中的系数1、2、1恰好对应图中第三行的数字；
再如，
展开式中的系数1、3、3、1恰好对应图中第四行的数字。
请认真观察此图，写出（a+b）4的展开式，（a+b）4=_______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
