
【题目】如图,数轴上![]() 、
、![]() 两点对应的有理数分別为
两点对应的有理数分別为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 分别同时从点
分别同时从点![]() 和点
和点![]() 出发,以每秒
出发,以每秒![]() 个单位长度,每秒
个单位长度,每秒![]() 个单位长度的速度向数轴正方向运动,设运动时间为
个单位长度的速度向数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)当![]() 时,则
时,则![]() 、
、![]() 两点对应的有理数分别是______;
两点对应的有理数分别是______;![]() _______;
_______;
(2)点![]() 是数轴上点
是数轴上点![]() 左侧一点,其对应的数是
左侧一点,其对应的数是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在点![]() 和点
和点![]() 出发的同时,点
出发的同时,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,开始向左运动,遇到点
出发,开始向左运动,遇到点![]() 后立即返回向右运动,遇到点
后立即返回向右运动,遇到点![]() 后立即返回向左运动,与点
后立即返回向左运动,与点![]() 相遇后再立即返回,如此往返,直到
相遇后再立即返回,如此往返,直到![]() 、
、![]() 两点相遇时,点
两点相遇时,点![]() 停止运动,求点
停止运动,求点![]() 运动的路程一共是多少个单位长度?点
运动的路程一共是多少个单位长度?点![]() 停止的位置所对应的数是多少?
停止的位置所对应的数是多少?
【答案】(1)24,8;16;(2)![]() 或10;(3)80;40.
或10;(3)80;40.
【解析】
(1)根据路程=速度×时间,先求出OQ,OP的值,进而可求出PQ的值.
(2)由CB=2CA,可得30-x=2(x-20)或30-x=2(20-x),解方程即可.
(3)设t秒后P、Q相遇.则有4t-2t=20,t=10,此时P、Q、R在同一点,由此可以确定点R的位置.
(1)t=2时,OQ=2×4=8,PA=2×2=4,OP=24,
∴P、Q分别表示24和8,PQ=24-8=16,
故答案为24,8;16.
(2)∵CB=2CA,
∴30-x=2(x-20)或30-x=2(20-x),
∴x=![]() 或10.
或10.
(3)设t秒后P、Q相遇.则有4t-2t=20,
∴t=10,
∴R运动的路程一共是8×10=80.
此时P、Q、R在同一点,所以点R的位置所对应的数是40.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.

解:∵AB∥CD(已知)
∴∠EFD=∠AEF( )
∵∠AEF=68°(已知)
∴∠EFD=∠AEF=68°( )
∵FG平分∠EFD(已知)
所以∠EFG=∠GFD=![]() ∠EFD=34°( )
∠EFD=34°( )
又因为KF⊥FG( )
所以∠KFG=90°( )
所以∠KFC=180°-∠GFD-∠KFG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
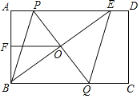
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系,并说明理由;
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国际无烟日”来临之际,小敏同学就一批公众对在餐厅吸烟所持的三种态度(彻底禁烟、建立吸烟室、其他)进行了调查,并把调查结果绘制成如图所示统计图,请根据图中的信息回答下列问题:

(1)被调查者中,不吸烟者中赞成“彻底禁烟”的人数有______人;
(2)本次抽样调查的样本容量为_______;
(3)被调查中,希望建立吸烟室的人数有______;
(4)某市现有人口约30万人,根据图中的信息估计赞成在餐厅彻底禁烟的人数约有______万人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图直线y=![]() x+2与抛物线y=ax2交于A.B两点,点B的坐标(3,m),直线AB交y轴于点C.
x+2与抛物线y=ax2交于A.B两点,点B的坐标(3,m),直线AB交y轴于点C.
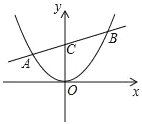

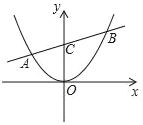
(1)求a,m的值;
(2)点P在对称轴右侧的抛物线上,设P点横坐标为t,△PAB的面积为s,求s与t的函数关系式;
(3)在(2)的条件下,在x轴上有一点Q,当以B.C.P.Q为顶点的四边形是平行四边形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD.

(1)如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;
(2)若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m取不同值时,二次函数y的图象与x轴的交点的个数情况;
(2)设二次函数的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com