
【题目】已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m取不同值时,二次函数y的图象与x轴的交点的个数情况;
(2)设二次函数的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的表达式.
【答案】答案见解析
【解析】整体分析:
(1)二次函数y的图象与x轴的交点的个数即是一元二次方程x2-(2m-1)x+m2+3m+4=0的根的个数;(2)由x12+x22=5,结合根与系数的关系,确定m的值,得到点C,M的坐标,即可求出直线CM的解析式.
解:(1)根据题意得,
[-(2m-1)]2-4×1×(m2+3m+4)=-16m-15,
当-16m-15>0,即m<![]() ,有两个交点;
,有两个交点;
当-16m-15=0,即m=![]() ,有一个交点;
,有一个交点;
当-16m-15<0,即m>![]() ,无交点.
,无交点.
(2)由根与系数的关系得x1+x2=2m-1,x1x2=m2+3m+4.
因为x12+x22=(x1+x2)2-2x1x2,
所以(2m-1)2-2(m2+3m+4)=5,解得m1=6,m2=-1,
因为m≤![]() ,所以m2=-1,
,所以m2=-1,
当m=-1时,二次函数的解析式为y=x2+3x+2,
则二次函数的解析式为y=x2+3x+2的图象与y轴的交点C(0,2),顶点M(![]() ,-
,-![]() ).
).
设一次函数的解析式为y=kx+2,则![]() =-
=-![]() ,解得x=
,解得x=![]() ,
,
所以y=![]() x+2.
x+2.
所以直线CM的表达式为y=![]() x+2.
x+2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() 、
、![]() 两点对应的有理数分別为
两点对应的有理数分別为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 分别同时从点
分别同时从点![]() 和点
和点![]() 出发,以每秒
出发,以每秒![]() 个单位长度,每秒
个单位长度,每秒![]() 个单位长度的速度向数轴正方向运动,设运动时间为
个单位长度的速度向数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)当![]() 时,则
时,则![]() 、
、![]() 两点对应的有理数分别是______;
两点对应的有理数分别是______;![]() _______;
_______;
(2)点![]() 是数轴上点
是数轴上点![]() 左侧一点,其对应的数是
左侧一点,其对应的数是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在点![]() 和点
和点![]() 出发的同时,点
出发的同时,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,开始向左运动,遇到点
出发,开始向左运动,遇到点![]() 后立即返回向右运动,遇到点
后立即返回向右运动,遇到点![]() 后立即返回向左运动,与点
后立即返回向左运动,与点![]() 相遇后再立即返回,如此往返,直到
相遇后再立即返回,如此往返,直到![]() 、
、![]() 两点相遇时,点
两点相遇时,点![]() 停止运动,求点
停止运动,求点![]() 运动的路程一共是多少个单位长度?点
运动的路程一共是多少个单位长度?点![]() 停止的位置所对应的数是多少?
停止的位置所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.

(1)图中除了△ABC与△ADC外,还有哪些三角形全等,请写出来;
(2)点P、Q在运动过程中,四边形APCQ的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)当点P在什么位置时,△PCQ的面积最大,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.

(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形![]() 为长方形,其中点
为长方形,其中点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,且
,且![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求![]() 两点坐标;
两点坐标;
(2)一动点![]() 从
从![]() 出发,以2个单位/秒的速度沿
出发,以2个单位/秒的速度沿![]() 向
向![]() 点运动(不与
点运动(不与![]() 点重合),在
点重合),在![]() 点运动过程中,连接
点运动过程中,连接![]() ,
,
①试探究![]() 之间的数量关系;并说明理由;
之间的数量关系;并说明理由;
②是否存在某一时刻![]() ,使三角形
,使三角形![]() 的面积等于长方形
的面积等于长方形![]() 面积的
面积的![]() ?若存在,求
?若存在,求![]() 的值并求此时点
的值并求此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
③三角形![]() 的面积记作
的面积记作![]() ;三角形
;三角形![]() 的面积记作
的面积记作![]() ;三角形
;三角形![]() 的面积记作
的面积记作![]() ;直接写出
;直接写出![]() 、
、![]() 、
、![]() 的关系.
的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
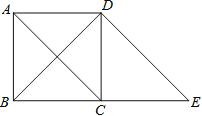
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频率分布表和频率直方图的一部分如下:
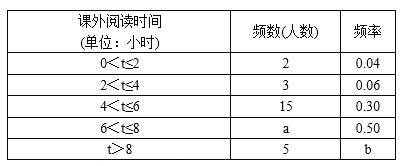
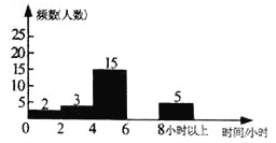
请根据图表信息回答下列问题:
(1)频数分布表中的a=____________,b=____________;
(2)将频数直方图补充完整;
(3)学校将每周课外阅读时间在6小时以上的学生评为“阅读之星”,请你估计该校2 000名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com