练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】尺规作图：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树．如图，要求桂花树的位置（视为点P），到花坛的两边AB、BC的距离相等，并且点P到点A、D的距离也相等．请用尺规作图作出栽种桂花树的位置点P（不写作法，保留作图痕迹）．

    【答案】作图见解析.

    【解析】试题分析：分别作出AD的垂直平分线及∠ABC的平分线，两条直线的交点即为P点的位置．

    试题解析：（1）①分别以A、D为圆心，以大于AD为半径画圆，两圆相交于E、F两点；

    ②连接EF，则EF即为线段AD的垂直平分线．

    （2）①以B为圆心，以大于任意长为半径画圆，分别交AB、BC为G、H；

    ②分别以G、H为圆心，以大于GH为半径画圆，两圆相交于点I，连接BI，则BI即为∠ABC的平分线．

    ③BI与EF相交于点P，则点P即为所求点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

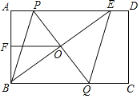
    【题目】如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD，BE，BC于点P，O，Q，连接BP，EQ．

    （1）求证：四边形BPEQ是菱形；

    （2）F为AB的中点，则线段OF与线段AE有什么位置关系和数量关系，并说明理由；

    （3）在（2）的条件下，若AB＝6，OF＝4，求PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形 是一个边长为 6 的正方形，点 在 的延长线上，连接 ，过作 的垂线，交 的延长线于点 ，且 ，则 _____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】O为直线AB上的一点，OC⊥OD，射线OE平分∠AOD.

    (1)如图①，判断∠COE和∠BOD之间的数量关系，并说明理由；

    (2)若将∠COD绕点O旋转至图②的位置，试问(1)中∠COE和∠BOD之间的数量关系是否发生变化？并说明理由；

    (3)若将∠COD绕点O旋转至图③的位置，探究∠COE和∠BOD之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请从以下四个一元二次方程中任选三个，并用适当的方法解这三个方程．

    （1）x2﹣x﹣1=0；

    （2）（y﹣2）2﹣12=0；

    （3）（1+m）2=m+1；

    （4）t2﹣4t=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一数值转换器，原理如图所示，若开始输入x的值是7，可发现第1次输出的结果是12，第2次输出的结果是6，第3次输出的结果是　　　　，依次继续下去…，第2013次输出的结果是　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

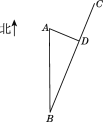
    【题目】如图，某沿海城市A接到台风警报，在该城市正南方向260 km的B处有一台风中心，沿BC方向以15 km/h的速度向C移动，已知城市A到BC的距离AD＝100 km，那么台风中心经过多长时间从B点移动到D点？如果在距台风中心30 km的圆形区域内都将受到台风的影响，正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的二次函数y＝x2－(2m－1)x＋m2＋3m＋4.

    (1)探究m取不同值时，二次函数y的图象与x轴的交点的个数情况；

    (2)设二次函数的图象与x轴的交点为A(x1，0)，B(x2，0)，且x12＋x22＝5，与y轴的交点为C，它的顶点为M，求直线CM的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

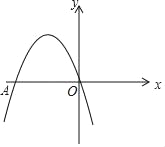
    【题目】如图，二次函数y=ax2﹣4x+c的图象经过坐标原点，与x轴交于点A（﹣4，0）

    （1）求此二次函数的解析式，并求出抛物线的顶点坐标；

    （2）在抛物线上存在点P，使△AOP的面积为10？求出点P的坐标．

    查看答案和解析>>

    同步练习册答案