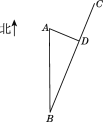
【题目】如图，某沿海城市A接到台风警报，在该城市正南方向260 km的B处有一台风中心，沿BC方向以15 km/h的速度向C移动，已知城市A到BC的距离AD＝100 km，那么台风中心经过多长时间从B点移动到D点？如果在距台风中心30 km的圆形区域内都将受到台风的影响，正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响？
培优好卷单元加期末卷系列答案科目：初中数学 来源： 题型：
【题目】如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数。
例如，
展开式中的系数1、2、1恰好对应图中第三行的数字；
再如，
展开式中的系数1、3、3、1恰好对应图中第四行的数字。
请认真观察此图，写出（a+b）4的展开式，（a+b）4=_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】尺规作图：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树．如图，要求桂花树的位置（视为点P），到花坛的两边AB、BC的距离相等，并且点P到点A、D的距离也相等．请用尺规作图作出栽种桂花树的位置点P（不写作法，保留作图痕迹）．
查看答案和解析>>
科目：初中数学 来源： 题型：
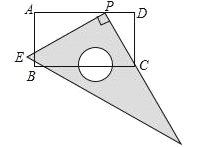
【题目】如图，在矩形ABCD中，AB=6，AD=11．直角尺的直角顶点P在AD上滑动时（点P与A，D不重合），一直角边始终经过点C，另一直角边与AB交于点E．
（1）△CDP与△PAE相似吗？如果相似，请写出证明过程；
（2）是否存在这样的点P，使△CDP的周长等于△PAE周长的2倍？若存在，求DP的长；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知菱形ABCD的边长为2，∠B=60°，点P、Q分别是边BC、CD上的动点（不与端点重合），且BP=CQ．
（1）图中除了△ABC与△ADC外，还有哪些三角形全等，请写出来；
（2）点P、Q在运动过程中，四边形APCQ的面积是否变化，如果变化，请说明理由；如果不变，请求出面积；
（3）当点P在什么位置时，△PCQ的面积最大，并请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=a．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．
（1）求证：△COD是等边三角形；
（2）当a=150°时，试判断△AOD的形状，并说明理由；
（3）探究：当a为多少度时，△AOD是等腰三角形？
查看答案和解析>>
科目：初中数学 来源： 题型：
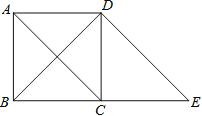
【题目】如图，过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E．
（1）判断四边形ACED的形状，并说明理由；
（2）若BD=8cm，求线段BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AB＝BC＝2CD，AB∥CD，∠C＝90°，E是BC的中点，AE与BD相交于点F，连接DE.
(1)求证：△ABE≌△BCD；
(2)判断线段AE与BD的数量关系及位置关系，并说明理由；
(3)若CD＝1，试求△AED的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
