
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
【答案】(1)∠A+∠C=90°;(2)见解析;(3)105°.
【解析】
(1)根据平行线的性质以及直角三角形的性质进行解答即可;
(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;
(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.
(1)如图1,∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
故答案为∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,
则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
在△BCF中,由∠CBF+∠BFC+∠BCF=180°,
可得 (2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.



科目:初中数学 来源: 题型:
【题目】“五一”期间,某商场推出“购物满额即可抽奖”活动.商场在抽奖箱中装有1个红球、2个黄球、3个白球、8个黑球,每个球除颜色外都相同,红球、黄球、白球分别代表一、二、三等奖,黑球代表谢谢参与.获得抽奖机会的顾客每次从箱子中摸出一个球,按相应颜色对应等级兑换奖品,每次所摸得球再放回抽奖箱,摇匀后由下一位顾客抽奖.已知小明获得1次抽奖机会.
(1)小明是否一定能中奖___________;(填是、否)
(2)求出小明抽到一等奖的概率;
(3)在这个活动中,中奖和没中奖的机会相等吗?为什么?如果不相等,可以如何改变球的个数,使中奖和没中奖的机会相等?(只写一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒。
秒。
(1)AC=______cm;
(2)若点P恰好在∠ABC的角平分线上,求此时![]() 的值;
的值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
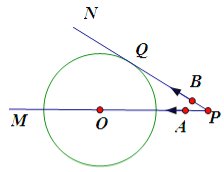
【题目】如图,已知⊙![]() 的半径为9cm,射线
的半径为9cm,射线![]() 经过点
经过点![]() ,OP=15 cm,射线
,OP=15 cm,射线![]() 与⊙
与⊙![]() 相切于点
相切于点![]() .动点
.动点![]() 自P点以
自P点以![]() cm/s的速度沿射线
cm/s的速度沿射线![]() 方向运动,同时动点
方向运动,同时动点![]() 也自P点以2cm/s的速度沿射线
也自P点以2cm/s的速度沿射线![]() 方向运动,则它们从点
方向运动,则它们从点![]() 出发 s后
出发 s后![]() 所在直线与⊙
所在直线与⊙![]() 相切.
相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地开展“阳光体育一小时”活动,对本校学生进行了“写出你最喜欢的体育活动项目(只写一项)”的随机抽样调查,下面是根据得到的相关数据绘制的统计图的一部分.
抽样调查学生最喜欢的运动项目的人数统计图 各运动项目的喜欢人数占抽样总人数百分比统计图

请根据以上信息解答下列问题:
(1)该校对________名学生进行了抽样调查;
(2)请将图1和图2补充完整;
(3)图2中跳绳所在的扇形对应的圆心角的度数是________;
(4)若该校共有2400名同学,请利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线.
(2)若AB=2![]() ,求OC的长.
,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图像经过点
的图像经过点![]() .
.
(![]() )求该二次函数的关系式.
)求该二次函数的关系式.
(![]() )证明:无论
)证明:无论![]() 取何值,函数值
取何值,函数值![]() 总不等于
总不等于![]() .
.
(![]() )将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
)将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com