
【题目】如图,已知⊙![]() 的半径为9cm,射线
的半径为9cm,射线![]() 经过点
经过点![]() ,OP=15 cm,射线
,OP=15 cm,射线![]() 与⊙
与⊙![]() 相切于点
相切于点![]() .动点
.动点![]() 自P点以
自P点以![]() cm/s的速度沿射线
cm/s的速度沿射线![]() 方向运动,同时动点
方向运动,同时动点![]() 也自P点以2cm/s的速度沿射线
也自P点以2cm/s的速度沿射线![]() 方向运动,则它们从点
方向运动,则它们从点![]() 出发 s后
出发 s后![]() 所在直线与⊙
所在直线与⊙![]() 相切.
相切.
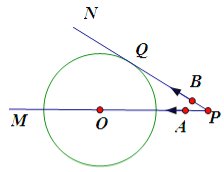
【答案】0.5s或10.5s.
【解析】
试题分析:PN与⊙O相切于点Q,OQ⊥PN,即∠OQP=90°,在直角△OPQ中根据勾股定理就可以求出PQ的值,过点O作OC⊥AB,垂足为C.直线AB与⊙O相切,则△PAB∽△POQ,根据相似三角形的对应边的比相等,就可以求出t的值.
试题解析: 连接OQ,
∵PN与⊙O相切于点Q,
∴OQ⊥PN,即∠OQP=90°,
∵OP=15,OQ=9,
∴PQ=![]() (cm).
(cm).
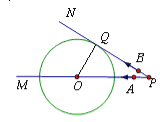
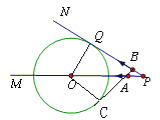
过点O作OC⊥AB,垂足为C,
∵点A的运动速度为![]() cm/s,点B的运动速度为2cm/s,运动时间为ts,
cm/s,点B的运动速度为2cm/s,运动时间为ts,
∴PA=![]() t,PB=2t,
t,PB=2t,
∵PO=15,PQ=12,
∴![]() ,
,
∵∠P=∠P,
∴△PAB∽△POQ,
∴∠PBA=∠PQO=90°,
∵∠BQO=∠CBQ=∠OCB=90°,
∴四边形OCBQ为矩形.
∴BQ=OC.
∵⊙O的半径为,
∴BQ=OC=9时,直线AB与⊙O相切.
①当AB运动到如图1所示的位置,
BQ=PQ-PB=12-2t,
∵BQ=9,
∴8-4t=9,
∴t=0.25(s).
②当AB运动到如图2所示的位置,
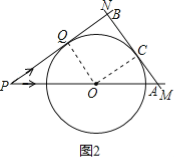
BQ=PB-PQ=2t-12,
∵BQ=9,
∴2t-12=9,
∴t=10.5(s).
∴当t为0.5s或10.5s时直线AB与⊙O相切.
考点: 1.切线的判定;2.勾股定理;3.矩形的性质;4.相似三角形的判定与性质.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶![]() ,AB=10米,AE=15米(i=1∶
,AB=10米,AE=15米(i=1∶![]() 是指坡面的铅直高度BH与水平长度AH的比).
是指坡面的铅直高度BH与水平长度AH的比).

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

⑴ 作出△![]() 绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标 .(写出一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴只有一个公共点.
轴只有一个公共点.
(![]() )求
)求![]() 的值.
的值.
(![]() )怎样平移抛物线
)怎样平移抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() ?请写出具体的平移方法.
?请写出具体的平移方法.
(![]() )若点
)若点![]() 和点
和点![]() 都在抛物线
都在抛物线![]() 上,且
上,且![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
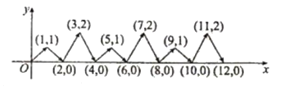
【题目】如图,一个动点P在平面直角坐标系中按箭头所示方向作折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),……,按这样的运动规律,经过第2013次运动后,动点P的坐标是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com