练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    以等边△ABC的三个顶点为圆心的⊙A、⊙B与⊙C，若其中⊙A与⊙B相外切，⊙A与⊙C也外切，而⊙B与⊙C相外离，则⊙A的半径RA与⊙B的半径RB之间的大小关系是


    1. A.
      RA＞RB
    2. B.
      RA=RB
    3. C.
      RA＜RB
    4. D.
      以上都有可能
    A
    分析：首先知道两圆的几种位置关系，它们的圆心距与半径之间的关系，然后比较两圆半径的大小．
    解答：∵⊙A与⊙B相外切，⊙A与⊙C也外切，
    ∴RA+RB=RA+RC，
    ∵⊙B与⊙C相外离，
    ∴RB+RC＜RA+RC，
    ∴RA＞RB．
    故选A．
    点评：本题主要考查圆与圆的位置关系，①外离，则d＞R+r；②外切，则d=R+r；③相交，则R-r＜d＜R+r；④内切，则d=R-r；⑤内含，则d＜R-r．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    6、以等边△ABC的三个顶点为圆心的⊙A、⊙B与⊙C，若其中⊙A与⊙B相外切，⊙A与⊙C也外切，而⊙B与⊙C相外离，则⊙A的半径RA与⊙B的半径RB之间的大小关系是（　　）

    查看答案和解析>>

    科目：初中数学 来源：中考加速卷　　数学 题型：044

    如图，分别以等边△ABC的三个顶点为圆心，边长a为半径作 弧AB、弧BC、弧CA．你有办法求出弧AB、弧BC、弧CA所围成的图形(曲边三角形)的面积吗？若有，请你求出．

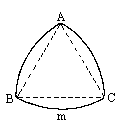
    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图，某市三个城镇中心A，B，C恰好分别位于一个等边三角形的三个顶点处，在三个城镇中心之间铺设通信光缆，以城镇A为出发点设计了三种连接方案：

    (1)AB＋BC；

    (2)AD＋BC(D为BC的中点)；

    (3)OA＋OB＋OC(O为△ABC三边的垂直平分线的交点)．要使铺设的光缆长度最短应选哪种方案？

    查看答案和解析>>

    科目：初中数学 来源：2010年上海市黄浦区中考数学二模试卷（解析版） 题型：选择题

    （2010•黄浦区二模）以等边△ABC的三个顶点为圆心的⊙A、⊙B与⊙C，若其中⊙A与⊙B相外切，⊙A与⊙C也外切，而⊙B与⊙C相外离，则⊙A的半径RA与⊙B的半径RB之间的大小关系是（ ）
    A．RA＞RB
    B．RA=RB
    C．RA＜RB
    D．以上都有可能

    查看答案和解析>>

    同步练习册答案