
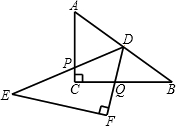
 如图,已知Rt△ABC≌Rt△DEF,∠C=∠F=90°,AC=DF=3,BC=EF=4,△DEF绕着斜边AB的中点D旋转,DE、DF分别交AC、BC所在的直线于点P,Q.当△BDQ为等腰三角形时,AP的长为________.
如图,已知Rt△ABC≌Rt△DEF,∠C=∠F=90°,AC=DF=3,BC=EF=4,△DEF绕着斜边AB的中点D旋转,DE、DF分别交AC、BC所在的直线于点P,Q.当△BDQ为等腰三角形时,AP的长为________. 或
或 或
或
 AC=
AC= ,BD=
,BD= AB=
AB= ,DN=BM=
,DN=BM= AC=2,可得到BQ与QM的长,然后利用等腰三角形的性质得到∠3=90°-
AC=2,可得到BQ与QM的长,然后利用等腰三角形的性质得到∠3=90°- ∠B,易得∠2=
∠B,易得∠2= ∠B,又Rt△ABC≌Rt△DEF,利用三角形全等的性质得到∠EDF=∠A=90°-∠B,则∠1=
∠B,又Rt△ABC≌Rt△DEF,利用三角形全等的性质得到∠EDF=∠A=90°-∠B,则∠1= ∠B,即∠1=∠2,则△CPD∽△CDA,然后根据三角形相似的性质得到PN:QM=DN:DM,代值计算可得CP,从而求得AP;
∠B,即∠1=∠2,则△CPD∽△CDA,然后根据三角形相似的性质得到PN:QM=DN:DM,代值计算可得CP,从而求得AP;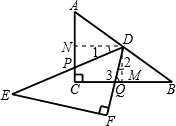 解:(1)当BD=BQ,
解:(1)当BD=BQ, AC=
AC= ,BD=
,BD= AB=
AB= ,DN=BM=
,DN=BM= AC=2,
AC=2, ,QM=
,QM= -2=
-2= ,
, ∠B,
∠B, ∠B,
∠B, ∠B,即∠1=∠2,
∠B,即∠1=∠2, =2:
=2: ,
, ,
, +
+ =
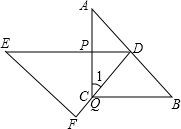
= ;
;
 ,
, =
= :3,
:3, ,
, =
= ;
;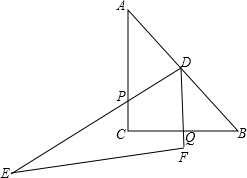
 :3,
:3, .
. 或
或 或
或 .
.

科目:初中数学 来源: 题型:
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.查看答案和解析>>
科目:初中数学 来源: 题型:
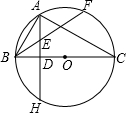 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE. |
| AB |
 |
| AF |
查看答案和解析>>
科目:初中数学 来源: 题型:
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com