
【题目】如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:① x + y=a;② x-y=b;③ a2-b2=2xy;④ x2-y2=ab;⑤ x2 + y2=![]() ,其中正确的有__________.
,其中正确的有__________.

【答案】①②④⑤
【解析】
利用大正方形的边长=长方形的长+长方形的宽,小正方形的边长=长方形的长-长方形的宽,大正方形的面积-小正方形的面积=4个长方形的面积,完全平方公式x2+y2=(x+y)2-2xy,进而判定即可.
由图形可得:①大正方形的边长=长方形的长+长方形的宽,故x+y=a正确;
②小正方形的边长=长方形的长-长方形的宽,故x-y=b正确;
③大正方形的面积-小正方形的面积=4个长方形的面积,故a2-b2=4xy错误;
④根据①知x+y=a,根据②知x-y=b,则x2-y2=ab,正确;
⑤x2+y2=(x+y)2-2xy=a2-2×![]() ,正确.
,正确.
所以正确的是①②④⑤.
故答案为:①②④⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1),B(﹣1,1),C(0,﹣2).
(1)写出点B关于坐标原点O对称的点B1的坐标;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B1的正比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形ABCD的宽AD=8,点E在边AB上,P为线段DE上的一动点(点P与点D,E不重合),∠MPN=90°,M,N分别在直线AB,CD上,过点P作直线HK ![]() AB,作PF⊥AB,垂足为点F,过点N作NG⊥HK,垂足为点G
AB,作PF⊥AB,垂足为点F,过点N作NG⊥HK,垂足为点G
(1)求证:∠MPF=∠GPN
(2)在图1中,将直角∠MPN绕点P顺时针旋转,在这一过程中,试观察、猜想:当MF=NG时,△MPN是什么特殊三角形?在图2中用直尺画出图形,并证明你的猜想;
(3)在(2)的条件下,当∠EDC=30°时,设EP=x,△MPN的面积为S,求出S关于x的解析式,并说明S是否存在最小值?若存在,求出此时x的值和△MPN面积的最小值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
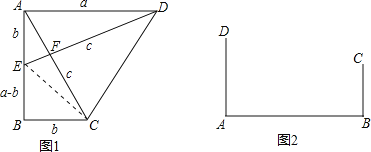
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-4x-m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用代数式表示:
(1)a,b两数的平方和减去它们乘积的2倍;
(2)a,b两数的和的平方减去它们的差的平方;
(3)一个两位数,个位上的数字为a,十位上的数字为b,请表示这个两位数;
(4)若a表示三位数,现把2放在它的右边,得到一个四位数,请表示这个四位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com