
【题目】如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
【答案】A
【解析】∵BE平分∠ABC,
∴∠ABE=∠CBE,
又∵∠BAD=∠C,
∴△BFA∽△BEC,
故B正确.
又∵∠BAD=∠C,∠ABC=∠ABD,
△BAC∽△BDA,
故C正确.
∴∠BFA=∠BEC,
又∵∠BFA+∠BFD=180°,∠BEC+∠BEA=180°,
∴∠BFD=∠BEA,
又∵∠DBF=∠ABE,
∴△BDF∽△BAE,
故D正确.
不能证明△BDF∽△BEC,故A错误.
所以答案是:A.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:① x + y=a;② x-y=b;③ a2-b2=2xy;④ x2-y2=ab;⑤ x2 + y2=![]() ,其中正确的有__________.
,其中正确的有__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90![]() ,射线OC绕点O从OA位置开始,以每秒4
,射线OC绕点O从OA位置开始,以每秒4![]() 的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1
的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1![]() 的速度逆时针方向旋转. 当OC与OA成180
的速度逆时针方向旋转. 当OC与OA成180![]() 时,OC与OD同时停止旋转.
时,OC与OD同时停止旋转.
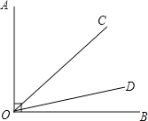
(1)当OC旋转10秒时,∠COD=___.
(2)当OC与OD的夹角是30![]() 时,求旋转的时间.
时,求旋转的时间.
(3)当OB平分∠COD时,求旋转的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x,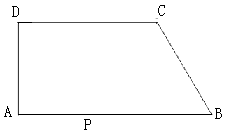
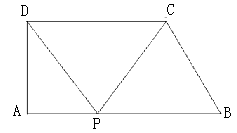
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)直接写出:当△CDP为等腰三角形时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
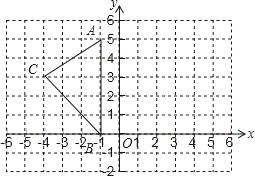
【题目】如图:在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)S△ABC= .
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1(其中点A、B、C的对称点分别为点A1、B1、C1).
(3)写出点A1、B1、C1的坐标.A1 ,B1 ,C1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由一副三角板拼成的图案,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求图1中![]() 的度数;
的度数;
(2)若将图1中的三角板![]() 不动,将另一三角板
不动,将另一三角板![]() 绕点
绕点![]() 顺时针或逆时针旋转
顺时针或逆时针旋转![]() 度(
度(![]() ).当
).当![]() 时,求
时,求![]() 的度数(图2,图3,图4仅供参考).
的度数(图2,图3,图4仅供参考).
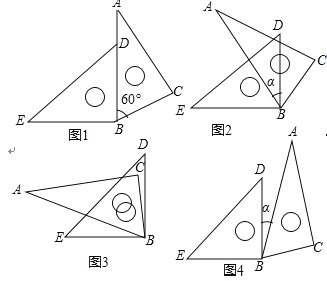
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )
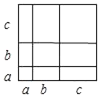
A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com