
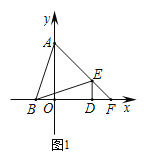
【题目】如图1,在平面直角坐标系中,点A(0,3),点B(-1,0),点D(2,0),DE⊥x轴且∠BED=∠ABD,延长AE交x轴于点F.
(1)求证:∠BAE=∠BEA;
(2)求点F的坐标;
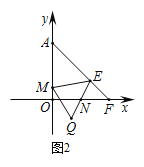
(3)如图2,若点Q(m,-1)在第四象限,点M在y轴的正半轴上,∠MEQ=∠OAF,设AM-MQ=n,求m与n的数量关系,并证明.
【答案】(1)证明见解析;(2)F(3,0);(3)m=n,证明见解析.
【解析】
(1)先证明△ABO≌△BED,从而得出AB=BE,然后根据等边对等角可得出结论;
(2)连接OE,设DF=x,先求出点E的坐标,再根据S△AOE+S△EOF=S△AOF可得出关于x的方程,求出x,从而可得出点F的坐标;
(3)过Q作QP∥x轴交y轴于P,过E作EG⊥OA,EH⊥PQ,垂足分别为G,H,在GA上截取GK=QH,先证明△EQH≌△EKG,再证明△KEM≌△QEM,得出MK=MQ,从而有AM-MQ=AM-MK=AK=n①;连接EP,证明△AEK≌△PEQ,从而有AK=PQ=m②,由①②即可得出结论.
解:(1)∵A(0,3),B(-1,0),D(2,0),
∴OB=1,OD=2,OA=3,
∴AO=BD,
又∠AOB=∠BDE=90°,∠BED=∠ABD,
∴△ABO≌△BED(AAS),
∴BA=BE,
∴∠BAE=∠BEA;
(2)由(1)知,△ABO≌△BED,
∴DE=BO=1,∴E(2,1),
连接OE,设DF=x,
∵S△AOE+S△EOF=S△AOF,
∴3×2×![]() +(2+x)×1×
+(2+x)×1×![]() =3(2+x)×
=3(2+x)×![]() ,
,
∴x=1,
∴点F的坐标为(3,0);
(3)m=n,证明如下:
∵OA=OF=3,∴∠OAF=45°=∠MEQ,
过Q作QP∥x轴交y轴于P,过E作EG⊥OA,EH⊥PQ,垂足分别为G,H,在GA上截取GK=QH,
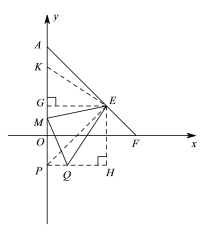
∵Q(m,-1),E(2,1),
∴EG=EH=PH=PG=2,
又GK=QH,∠EGK=∠EQH=90°,
∴△EQH≌△EKG(SAS),
∴EK=EQ,∠GEK=∠HEQ,
∵∠GEH=90°,∠MEQ=45°,∴∠QEH+∠GEM=45°,∴∠GEK+∠GEM=45°,
即∠KEM=45°=∠MEQ,
又EM=EM,
∴△KEM≌△QEM(SAS),∴MK=MQ,
∴AM-MQ=AM-MK=AK=n①,
∴MQ=MG+KG=MG+QH.
连接EP,△EHP为等腰直角三角形,∠EPH=45°,
∴∠EPQ=∠EPA=45°,△EHP为等腰直角三角形,PE=AE,∠PEA=90°,∵∠KEM=∠MEQ=45°,∴∠KEQ=90°,
∴∠AEK=∠PEQ,∠EPQ=∠KAE,
∴△AEK≌△PEQ,
∴AK=PQ=m②,
由①②可得,m=n.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
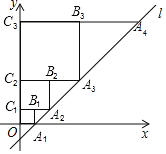
【题目】在平面直角坐标系xOy中,直线l:y=2x﹣2与x轴交于点A1,如图所示,依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnnCn﹣1,使得点A1,A2,A3,…An在直线l上,点C1,C2,C3,…n在y轴正半轴上,则正方形AnBnnCn﹣1的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家看过中央电视台“购物街”节目吗?其中有一个游戏环节是大转轮比赛,转轮上平均分布着5、10、15、20一直到100共20个数字.选手依次转动转轮,每个人最多有两次机会.选手转动的数字之和最大不超过100者为胜出;若超过100则成绩无效,称为“爆掉”.
(1)某选手第一次转到了数字5,再转第二次,则他两次数字之和为100的可能性有多大?
(2)现在某选手第一次转到了数字65,若再转第二次了则有可能“爆掉”,请你分析“爆掉”的可能性有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中,![]() ,对角线
,对角线![]() 于
于![]() 点,点
点,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上.
轴上.
![]() 若
若![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 若
若![]() ,
,![]() ,求过
,求过![]() 点的反比例函数的解析式;
点的反比例函数的解析式;
![]() 如图,在
如图,在![]() 上有一点
上有一点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在
,在![]() 上取
上取![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,(不与
上运动时,(不与![]() 、
、![]() 重合),
重合),![]() 的值是否发生变化?若变化,求出变化范围;若不变,求出其值.
的值是否发生变化?若变化,求出变化范围;若不变,求出其值.


查看答案和解析>>
科目:初中数学 来源: 题型:
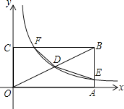
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 为对角线
为对角线![]() 的中点,反比例函数
的中点,反比例函数![]() 在第一象限内的图象经过点
在第一象限内的图象经过点![]() ,且与
,且与![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 两点,若四边形
两点,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
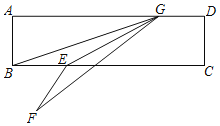
【题目】如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=3,点E是线段BC上的一个动点(点E不与点B、C重合),连接GB、GE,△GBE与△GFE关于直线GE对称,当点F落在直线BC和直线DC上时,则所有满足条件的线段BE的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形BEFG的边长分别为1和3,点C在边BG上,线段DF、EG交于点M,连接DE、BM,则△DEG的面积为____,BM=____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com