
【题目】如图,正方形ABCD和正方形BEFG的边长分别为1和3,点C在边BG上,线段DF、EG交于点M,连接DE、BM,则△DEG的面积为____,BM=____.

【答案】![]()
![]() .
.
【解析】
依据五边形AEFGD的面积减去△ADE和△EFG的面积,即可得到△DEG的面积;连接BD,BF,即可得到△BDF是直角三角形,然后证明M是DF的中点,再根据勾股定理求出DF的长,依据直角三角形斜边上中线的性质即可得出BM的长.
根据题意得:△DEG的面积为:12+32![]() 1×(3﹣1)
1×(3﹣1)![]() 1×(1+3)
1×(1+3)![]() 32=1+9+1﹣2
32=1+9+1﹣2![]() ,
,
如图,连接BD,BF,则∠DBF=90°,
∴△BDF是直角三角形.
∵BM与FM关于GE对称,
∴BM=FM,
∴∠MBF=∠MFB,
又∵∠MBF+∠MBD=∠MFB+∠MDB,
∴∠MDB=∠MBD,
∴DM=BM,
∴M是DF的中点,
∴Rt△BDF中,BM![]() DF.
DF.
∵正方形ABCD和正方形BEFG的边长分别为1和3,
∴BD![]() ,BF=3
,BF=3![]() ,
,
∴DF![]() 2
2![]() ,
,
∴BM![]() .
.
故答案为:![]() ,
,![]() .
.



科目:初中数学 来源: 题型:
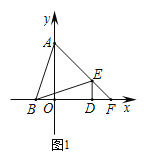
【题目】如图1,在平面直角坐标系中,点A(0,3),点B(-1,0),点D(2,0),DE⊥x轴且∠BED=∠ABD,延长AE交x轴于点F.
(1)求证:∠BAE=∠BEA;
(2)求点F的坐标;
(3)如图2,若点Q(m,-1)在第四象限,点M在y轴的正半轴上,∠MEQ=∠OAF,设AM-MQ=n,求m与n的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市2013年体育中考考试方案公布后,同学们将根据自己平的运动成绩确定自己的报考项目,下面是小亮同学近期在两个项目中连续五次测试的(得分情况得分统计表得分折线图)
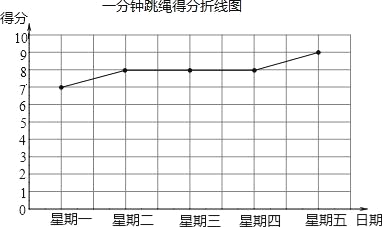
立定跳远测试日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
(1)请根据图表信息,分别计算小亮这两个项目测试成绩的平均数和方差;
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的报考项目?并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD的对角线交于点O,点E是边AB上一动点,点F在边BC上,且满足OE⊥OF,在点E由A运动到B的过程中,以下结论正确的个数为( )
①线段OE的大小先变小后变大;②线段EF的大小先变大后变小;③四边形OEBF的面积先变大后变小.
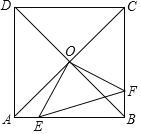
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O,⊙O与AC的公共点为E,连接DE并延长交BC的延长线于点F,BD=BF.
(1)试判断AC与⊙O的位置关系并说明理由;
(2)若AB=12,BC=6,求⊙O的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 ![]() ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
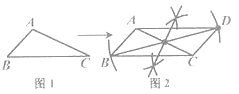
A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形 D. 对角线互相平分的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①所示的三角形纸片内部有一点P.
任务:借助折纸在纸片上画出过点P与BC边平行的线段FG.
阅读操作步骤并填空:
小谢按图①~图④所示步骤进行折纸操作完成了画图任务.
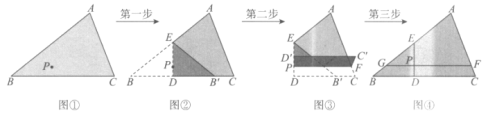
在小谢的折叠操作过程中,
(1)第一步得到图②,方法是:过点P折叠纸片,使得点B落在BC边上,落点记为![]() ,折痕分别交原AB,BC边于点E,D,此时∠
,折痕分别交原AB,BC边于点E,D,此时∠![]() 即∠
即∠![]() =__________°;
=__________°;
(2)第二步得到图③,参考第一步中横线上的叙述,第二步的操作指令可叙述为:_____________,并求∠EPF的度数;
(3)第三步展平纸片并画出两次折痕所在的线段ED,FG得到图④.
完成操作中的说理:
请结合以上信息证明FG∥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com