
【题目】已知 ![]() ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
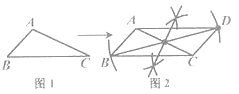
A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形 D. 对角线互相平分的四边形是平行四边形
科目:初中数学 来源: 题型:
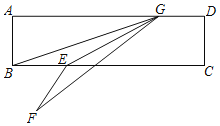
【题目】如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=3,点E是线段BC上的一个动点(点E不与点B、C重合),连接GB、GE,△GBE与△GFE关于直线GE对称,当点F落在直线BC和直线DC上时,则所有满足条件的线段BE的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形BEFG的边长分别为1和3,点C在边BG上,线段DF、EG交于点M,连接DE、BM,则△DEG的面积为____,BM=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
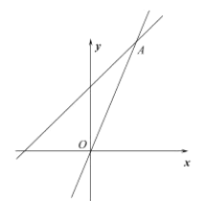
【题目】如图,一次函数![]() 的图像与正比例函数
的图像与正比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像都经过
)的图像都经过![]() .
.
(1)求点![]() 的坐标及正比例函数的表达式;
的坐标及正比例函数的表达式;
(2)利用函数图像比较![]() 和
和![]() 的大小并直接写出对应的
的大小并直接写出对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小梅、小花四人共同探究代数式x2-4x+5的值的情况,他们作了如下分工:小明负责找值为1时的x值,小亮负责找值为0时的x值,小梅负责找最小值,小花负责找最大值.几分钟后,各自通报探究的结论,其中错误的是( )
A.小明认为只有当x=2时,x2-4x+5的值为1;
B.小亮认为找不到实数x,使x2-4x+5的值为0;
C.小花发现当取大于2的实数时,x2-4x+5的值随x的增大而增大,因此认为没有最大值;
D.小梅发现x2-4x+5的值随x的变化而变化,因此认为没有最小值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(1,2)、B(–1,–2)是函数![]() 的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则( )
的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则( )
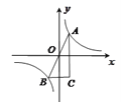
A. S = 2 B. S = 4 C. S = 8 D. S = 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,A,B两地相距60km,甲、乙分别从A,B两地出发,相向而行,图2中的![]() ,
,![]() 分别表示甲、乙离B地的距离y(km)与甲出发后所用的时间x(h)的函数关系.以下结论正确的是( )
分别表示甲、乙离B地的距离y(km)与甲出发后所用的时间x(h)的函数关系.以下结论正确的是( )
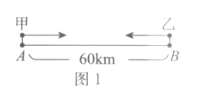
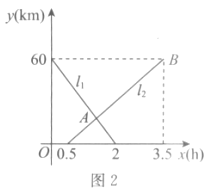
A.甲的速度为20km/h
B.甲和乙同时出发
C.甲出发1.4h时与乙相遇
D.乙出发3.5h时到达A地
查看答案和解析>>
科目:初中数学 来源: 题型:
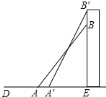
【题目】一根竹竿长![]() 米,先像
米,先像![]() 靠墙放置,与水平夹角为
靠墙放置,与水平夹角为![]() ,为了减少占地空间,现将竹竿像
,为了减少占地空间,现将竹竿像![]() 放置,与水平夹角为
放置,与水平夹角为![]() ,则竹竿让出多少水平空间( )
,则竹竿让出多少水平空间( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com