
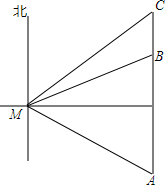
 如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时.
如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时. 分析 (1)如图,由题意得到∠A=∠DMA=∠C=∠CMD=45°,∠MBD=60°,求得CD=DM=AD,MD⊥AC,在Rt△BMD中,由tan∠MBD=$\frac{DM}{BD}$=$\sqrt{3}$,于是得到BD=$\frac{\sqrt{3}}{3}$DM,即可得到结论;
(2)根据AD=DM=5(3+$\sqrt{3}$),BD=5($\sqrt{3}$+1)求出AB=AD+BD=10$\sqrt{3}$+20,即可得到结果.
解答 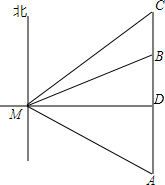 解:(1)如图,由题意得:∠A=∠DMA=∠C=∠CMD=45°,∠MBD=60°,
解:(1)如图,由题意得:∠A=∠DMA=∠C=∠CMD=45°,∠MBD=60°,
∴CD=DM=AD,MD⊥AC,
在Rt△BMD中,tan∠MBD=$\frac{DM}{BD}$=$\sqrt{3}$,
∴BD=$\frac{\sqrt{3}}{3}$DM,
∵BC=20×$\frac{1}{2}$=10,
∴CD-BD=DM-$\frac{\sqrt{3}}{3}$DM=10,
∴DM=5(3+$\sqrt{3}$),
答:渔船从A到B的航行过程中与小岛M之间的最短距离是5(3+$\sqrt{3}$)(海里);
(2)∵AD=DM=5(3+$\sqrt{3}$),BD=5($\sqrt{3}$+1)
∴AB=AD+BD=10$\sqrt{3}$+20,
∴渔船从A航行到B所用的时间为:$\frac{10\sqrt{3}+20}{20}$≈1.9(小时).
答:渔船从A航行到B所用的时间约为1.9小时.
点评 本题考查了解直角三角形的应用---方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.


科目:初中数学 来源: 题型:解答题
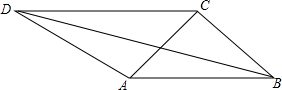 如图,已知CA=CB,∠ACB=90°,∠CBD=30°,CD∥AB.
如图,已知CA=CB,∠ACB=90°,∠CBD=30°,CD∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
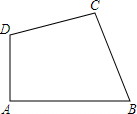 已知,如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5
已知,如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com