

分析 (1)如图1,过F作FH∥AB.根据平行线的性质得到∠1=∠2,∠3=∠FDC,由等量代换得到∠BFC=∠ABE+∠FCD,即可得到结论;
(2)设∠BCP=∠DCP=x,∠ABE=∠PBF=y,∠PCF=z,根据已知条件得到x+z=2y,即2y-z=x,由(1)知,∠AEB=∠ABE+∠DCF=x+y,∠E=∠PBF+∠DCF=∠PBF+∠DCP-∠PCF=x+y-z,于是得到2(∠BMC+∠E)=2(x+y+y+x-z)=2(2x+x)=6x,等量代换即可得到结论.
解答 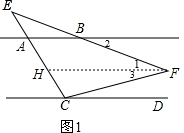 解:(1)如图1,过F作FH∥AB.
解:(1)如图1,过F作FH∥AB.
∵AB∥CD,
∴FH∥CD,
∴∠1=∠2,∠3=∠FDC,
∵∠2=∠ABE,
∴∠1=∠ABE,
∵∠BFC=∠1+∠3,
∴∠BFC=∠ABE+∠FCD,
∵∠AEB=∠BFC,
∴∠AEB=∠ABE+∠DCF;
(2)设∠BCP=∠DCP=x,∠ABE=∠PBF=y,∠PCF=z,
∵∠BCF=2∠ABE,
∴x+z=2y,即2y-z=x,
由(1)知,∠AEB=∠ABE+∠DCF=x+y,∠E=∠PBF+∠DCF=∠PBF+∠DCP-∠PCF=x+y-z,
∴2(∠BMC+∠E)=2(x+y+y+x-z)=2(2x+x)=6x,
∵3∠CAB=3(∠E+∠ABE)=3(x+y-z+y)=3(x+x)=6x,
∴2(∠BMC+∠AEB)=3∠CAB.
点评 本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
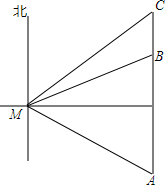 如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时.
如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com