
分析 (1)根据一元一次方程的定义,可得关于a的方程,根据解方程,可得答案;
(2)根据a的值,可得一元二次方程;
(3)根据把x的值代入方程检验,可得答案.
解答 解:(1)由(a+1)x|a|-4=2是关于x的一元一次方程,得
$\left\{\begin{array}{l}{|a|=1}\\{a+1≠0}\end{array}\right.$,
解得a=1;
(2)当a=1时,方程为2x-4=2;
(2)当x=-1时,左边=-2-4=-6,左边≠右边,x=-1不是方程的解;
当x=3时,左边=6-4=2,左边=右边,x=3是方程的解.
点评 本题主要考查了一元一次方程的一般形式,只含有一个未知数,且未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 己知数轴上顺次有A,B,C三点,分别表示数a,b,c,并且满足(a+24)2+|b+10|=0,b与c互为相反数,两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为6个单位/秒.
己知数轴上顺次有A,B,C三点,分别表示数a,b,c,并且满足(a+24)2+|b+10|=0,b与c互为相反数,两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为6个单位/秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
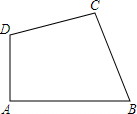 已知,如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5
已知,如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com